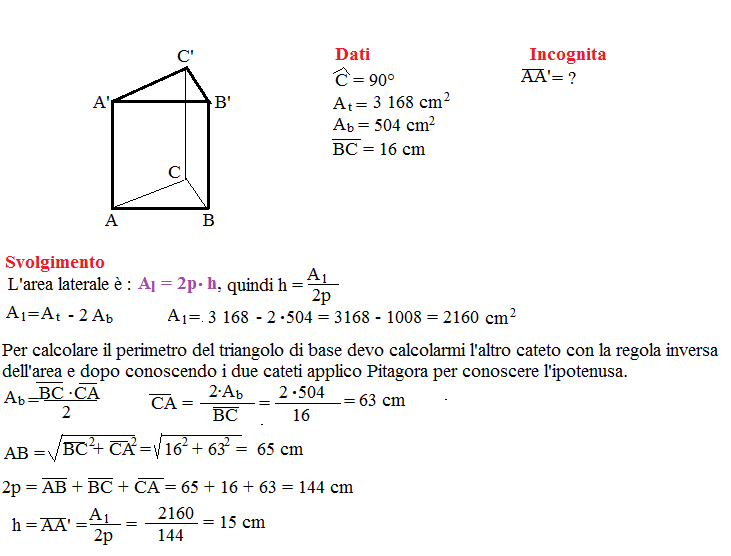
Come Si Calcola L'altezza Di Un Prisma

L'altezza di un prisma è una dimensione fondamentale che ne determina il volume e le proprietà. Si tratta, in termini semplici, della distanza perpendicolare tra le due basi del prisma, che sono poligoni congruenti e paralleli.
Comprendere l'Altezza di un Prisma
Cos'è l'altezza?
L'altezza di un prisma (spesso indicata con la lettera 'h') è la lunghezza del segmento di retta che connette le due basi perpendicolarmente. Immagina di 'impilare' una base sull'altra; l'altezza è quanto è alta questa pila. E' essenziale distinguerla dagli altri lati del prisma, soprattutto se si tratta di un prisma obliquo (non retto), dove le facce laterali non sono perpendicolari alle basi.
Perché l'altezza è importante?
L'altezza è cruciale per calcolare il volume del prisma. Il volume, che rappresenta lo spazio tridimensionale occupato dal prisma, si ottiene moltiplicando l'area della base per l'altezza. Senza conoscere l'altezza, non si può determinare il volume con precisione. Inoltre, l'altezza è necessaria per calcolare l'area superficiale laterale, che contribuisce all'area totale del prisma.
Come l'altezza influisce sugli studenti?
La comprensione dell'altezza di un prisma è fondamentale per gli studenti che si avvicinano alla geometria solida. Spesso, la difficoltà risiede nel visualizzare la dimensione corretta, specialmente quando il prisma è rappresentato in una figura bidimensionale. Una comprensione solida di questo concetto permette di risolvere problemi di geometria più complessi e di applicare le conoscenze acquisite in contesti pratici.
Metodi di Calcolo dell'Altezza
Il metodo per calcolare l'altezza di un prisma dipende dalle informazioni disponibili. Ecco alcuni scenari comuni:
Caso 1: Conoscendo il Volume e l'Area della Base
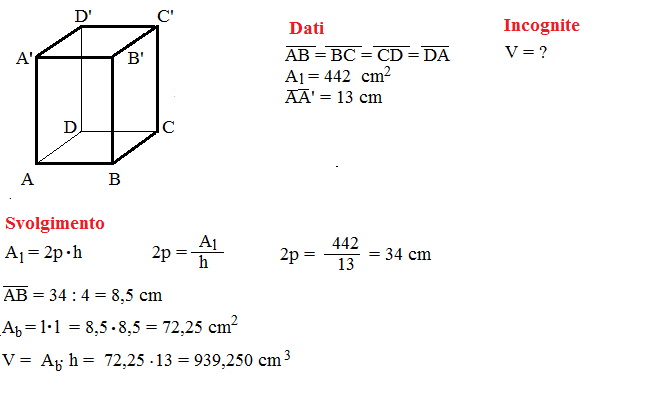
Se conosciamo il volume (V) del prisma e l'area (A) della sua base, possiamo usare la seguente formula: h = V / A. Questa formula deriva direttamente dalla formula del volume del prisma (V = A * h). È sufficiente dividere il volume per l'area della base per ottenere l'altezza.
Caso 2: Prisma Retto e Triangolo Rettangolo
Se il prisma è retto e si conosce la lunghezza di un lato della faccia laterale e l'angolo che questo lato forma con la base, si può usare la trigonometria. Se l è la lunghezza del lato e θ è l'angolo, allora: h = l * sin(θ). Questo metodo si basa sulla relazione trigonometrica tra il seno di un angolo, il lato opposto (l'altezza) e l'ipotenusa (il lato della faccia laterale).
Caso 3: Altre Informazioni Geometriche
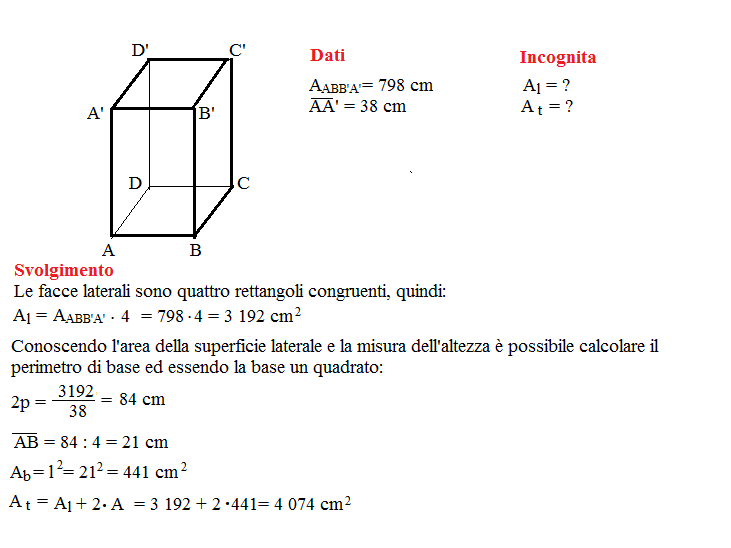
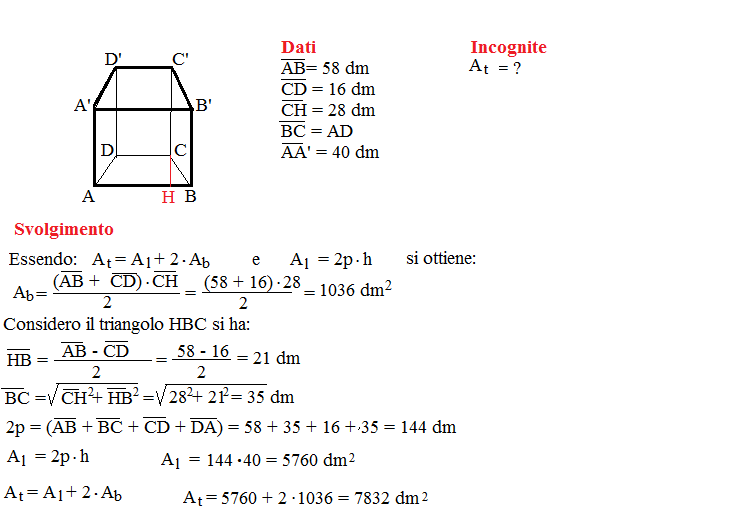
In alcuni problemi, potrebbero essere fornite informazioni aggiuntive sulle relazioni tra l'altezza, i lati delle basi e altre proprietà geometriche del prisma. In questi casi, è necessario utilizzare le proprietà geometriche del prisma e applicare teoremi come il teorema di Pitagora o relazioni trigonometriche per dedurre l'altezza. Per esempio, se si conosce la diagonale di una faccia laterale e la lunghezza di un lato della base, si potrebbe applicare il teorema di Pitagora per trovare l'altezza.
Applicazioni Pratiche
La comprensione dell'altezza di un prisma ha applicazioni pratiche sia in ambito scolastico che nella vita quotidiana. Ad esempio:
- Architettura e Ingegneria: Gli architetti e gli ingegneri utilizzano i principi della geometria solida per progettare edifici, ponti e altre strutture. La conoscenza dell'altezza dei prismi è essenziale per calcolare il volume dei materiali necessari e per garantire la stabilità delle strutture.
- Imballaggio: Le aziende che producono imballaggi utilizzano la geometria solida per ottimizzare le dimensioni delle scatole e dei contenitori. La conoscenza dell'altezza dei prismi consente di ridurre al minimo gli sprechi di materiale e di massimizzare lo spazio di stoccaggio.
- Vita Quotidiana: Anche nella vita quotidiana, la conoscenza dell'altezza dei prismi può essere utile. Ad esempio, quando si acquista un acquario, è importante conoscere le dimensioni del prisma per assicurarsi che si adatti allo spazio disponibile e per calcolare la quantità di acqua necessaria.
In conclusione, l'altezza di un prisma è un concetto chiave nella geometria solida con importanti applicazioni pratiche. Una comprensione solida di questo concetto è essenziale per gli studenti per affrontare con successo i problemi di geometria e per applicare le conoscenze acquisite in contesti reali.