Come Si Calcola La Tensione Della Fune

Ti sei mai chiesto quanta forza sta sopportando una fune mentre solleva un oggetto pesante, o magari la corda di un'altalena mentre ti dondoli? Comprendere come calcolare la tensione della fune è fondamentale in svariati campi, dall'ingegneria alla fisica, e può persino essere utile nella vita di tutti i giorni. Questo articolo è pensato per chiunque sia curioso di scoprire i segreti dietro la tensione nelle funi, che tu sia uno studente, un appassionato di fai-da-te o semplicemente qualcuno interessato a capire meglio il mondo che ti circonda. Cercheremo di rendere i concetti il più chiari e accessibili possibile, senza rinunciare alla precisione.

Cos'è la Tensione in una Fune?

La tensione in una fune, in termini semplici, è la forza di trazione esercitata dalla fune su qualsiasi oggetto a cui è collegata. Immagina di tirare una corda: la tensione è proprio la forza che senti, quella che ti permette di sollevare o spostare qualcosa. È importante capire che la tensione è una forza e, come tale, viene misurata in Newton (N) nel Sistema Internazionale.

La tensione si propaga attraverso la fune. In una fune ideale (senza massa e perfettamente flessibile), la tensione è costante in ogni punto della fune. Nella realtà, però, il peso della fune stessa e l'attrito possono influenzare la tensione, seppur in misura solitamente trascurabile per funi relativamente leggere.

Fattori che Influenzano la Tensione

Peso dell'oggetto: Maggiore è il peso dell'oggetto sospeso, maggiore sarà la tensione nella fune.
Angolo: Se la fune è inclinata, la tensione sarà influenzata dall'angolo di inclinazione.
Accelerazione: Se l'oggetto viene accelerato (ad esempio, sollevato rapidamente), la tensione aumenterà per tener conto dell'accelerazione.
Presenza di carrucole: Le carrucole possono modificare la direzione della forza e, di conseguenza, la tensione richiesta per sollevare un oggetto.

Come Calcolare la Tensione: Scenari Semplici

Iniziamo con alcuni scenari di base per comprendere i principi fondamentali.

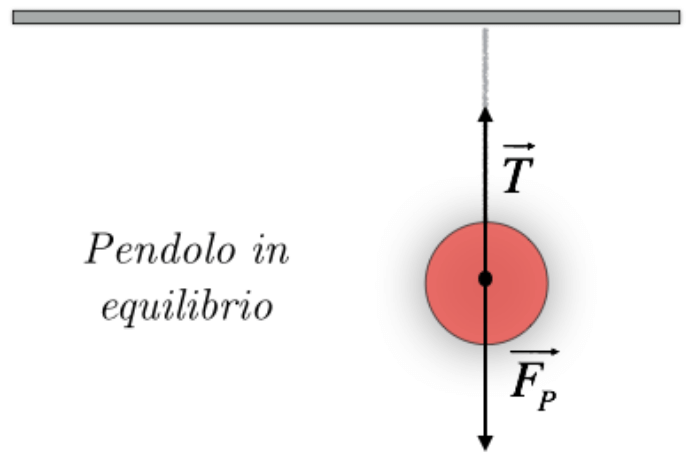
Caso 1: Oggetto Sospeso Verticalmente

Questo è il caso più semplice. Immagina una fune che sostiene un oggetto di peso noto. La tensione nella fune sarà uguale al peso dell'oggetto. Questo perché la tensione deve bilanciare la forza di gravità che agisce sull'oggetto per mantenerlo in equilibrio.

La formula è: T = mg

Dove:

T = Tensione (in Newton)
m = Massa dell'oggetto (in chilogrammi)
g = Accelerazione di gravità (circa 9.81 m/s²)

Esempio: Se un oggetto ha una massa di 10 kg, la tensione nella fune sarà T = 10 kg * 9.81 m/s² = 98.1 N.

Caso 2: Oggetto Tirato Orizzontalmente

Se stai tirando un oggetto orizzontalmente con una fune su una superficie senza attrito (un'idealizzazione, ovviamente), la tensione nella fune sarà uguale alla forza che stai applicando per tirare l'oggetto. Se l'oggetto è in movimento a velocità costante, la forza che applichi deve essere sufficiente a bilanciare eventuali forze di attrito.

La formula è: T = F

Dove:

T = Tensione (in Newton)
F = Forza applicata (in Newton)

Esempio: Se stai tirando un carrello con una forza di 50 N, la tensione nella fune sarà di 50 N.

Calcoli Più Complessi: Angoli e Componenti

Le cose si fanno più interessanti (e un po' più complesse) quando la fune è inclinata rispetto alla verticale o all'orizzontale. In questi casi, dobbiamo scomporre la tensione nelle sue componenti orizzontali e verticali.

Scomposizione della Tensione

Immagina una fune che tira un oggetto con un angolo θ rispetto all'orizzontale. La tensione (T) può essere scomposta in:

Componente orizzontale (Tx): Tx = T * cos(θ)
Componente verticale (Ty): Ty = T * sin(θ)

Queste componenti ci permettono di analizzare separatamente l'effetto della tensione nelle direzioni orizzontale e verticale.

Caso 3: Oggetto Sospeso da Due Funi

Questo è un esempio comune. Immagina un lampadario appeso al soffitto tramite due funi che formano un angolo. La tensione in ciascuna fune non sarà semplicemente la metà del peso del lampadario, a causa dell'angolo.

Per risolvere questo problema, dobbiamo considerare le componenti verticali delle tensioni nelle due funi. La somma delle componenti verticali deve essere uguale al peso del lampadario per mantenerlo in equilibrio.

Supponiamo che le due funi formino angoli θ1 e θ2 rispetto all'orizzontale, e che le tensioni nelle funi siano T1 e T2 rispettivamente. Allora:

T1 * sin(θ1) + T2 * sin(θ2) = mg

Inoltre, se il lampadario è in equilibrio orizzontale, le componenti orizzontali delle tensioni devono essere uguali e opposte:

T1 * cos(θ1) = T2 * cos(θ2)

Con queste due equazioni, possiamo risolvere per T1 e T2 se conosciamo gli angoli e il peso del lampadario. Questi calcoli richiedono una buona comprensione della trigonometria.

Caso 4: Carrucole

Le carrucole sono dispositivi che ci permettono di cambiare la direzione della forza. Un sistema di carrucole può anche ridurre la forza necessaria per sollevare un oggetto, a scapito di una maggiore lunghezza di corda tirata.

La carrucola fissa cambia solo la direzione della forza, senza ridurre la forza necessaria. La tensione nella fune rimane uguale al peso dell'oggetto.

La carrucola mobile, invece, riduce la forza necessaria per sollevare l'oggetto. Idealmente, con una carrucola mobile, la forza necessaria è la metà del peso dell'oggetto (trascurando l'attrito e il peso della carrucola stessa). In questo caso, la tensione nella fune è la metà del peso dell'oggetto.

I sistemi di carrucole più complessi combinano carrucole fisse e mobili per ottenere vantaggi ancora maggiori in termini di riduzione della forza. Il calcolo della tensione in questi sistemi richiede un'analisi attenta della disposizione delle funi e delle carrucole.

Consigli Pratici e Considerazioni Importanti

Sicurezza: Quando si lavora con funi e carichi pesanti, la sicurezza deve essere la priorità assoluta. Assicurati di utilizzare funi adatte al carico previsto e di controllare regolarmente lo stato delle funi per eventuali segni di usura o danneggiamento.
Attrito: Nei nostri calcoli, spesso abbiamo trascurato l'attrito. Nella realtà, l'attrito può influenzare la tensione nella fune, soprattutto nei sistemi di carrucole. Considera l'attrito se la precisione è fondamentale.
Flessibilità della Fune: Abbiamo assunto che le funi siano perfettamente flessibili. In realtà, le funi hanno una certa rigidità, che può influenzare la distribuzione della tensione.
Peso della Fune: Per funi molto lunghe o pesanti, il peso della fune stessa può diventare significativo e deve essere preso in considerazione nel calcolo della tensione.
Unità di Misura: Assicurati di utilizzare unità di misura coerenti (SI) per tutte le grandezze.

Applicazioni Reali

La comprensione della tensione nelle funi ha applicazioni in una vasta gamma di settori:

Ingegneria Civile: Progettazione di ponti sospesi, gru, funivie.
Ingegneria Meccanica: Progettazione di sistemi di sollevamento, ascensori.
Edilizia: Sollevamento di materiali da costruzione.
Arrampicata: Calcolo della sicurezza delle corde.
Nautica: Gestione delle vele e delle cime.
Sport: Progettazione di attrezzature sportive, come slackline e teleferiche.

Anche nella vita di tutti i giorni, una comprensione di base della tensione può essere utile, ad esempio, quando si appendono quadri pesanti, si montano tende da sole o si fissano oggetti sul tetto dell'auto.

In Conclusione

Speriamo che questo articolo ti abbia fornito una solida base per comprendere come calcolare la tensione della fune. Abbiamo visto che la tensione è una forza fondamentale che gioca un ruolo cruciale in molti sistemi meccanici. Partendo da scenari semplici, come un oggetto sospeso verticalmente, fino ad arrivare a calcoli più complessi che coinvolgono angoli e carrucole, abbiamo esplorato i principi chiave e le formule necessarie per determinare la tensione. Ricorda sempre di considerare i fattori che influenzano la tensione, come il peso dell'oggetto, l'angolo di inclinazione e l'attrito, e di dare la priorità alla sicurezza quando lavori con funi e carichi pesanti. Comprendere la tensione ti darà una maggiore consapevolezza del mondo che ti circonda e ti permetterà di affrontare con più sicurezza e competenza una varietà di situazioni pratiche.