Come Si Calcola L Area Di Un Triangolo Isoscele
Un triangolo isoscele è un triangolo che possiede due lati di uguale lunghezza. La sua caratteristica principale risiede nella simmetria attorno all'asse che divide a metà la base (il lato diseguale) e che interseca il vertice opposto. Calcolare l'area di un triangolo isoscele è un'operazione fondamentale in geometria e trova applicazioni in diversi contesti.
L'Area del Triangolo Isoscele: Concetti Chiave
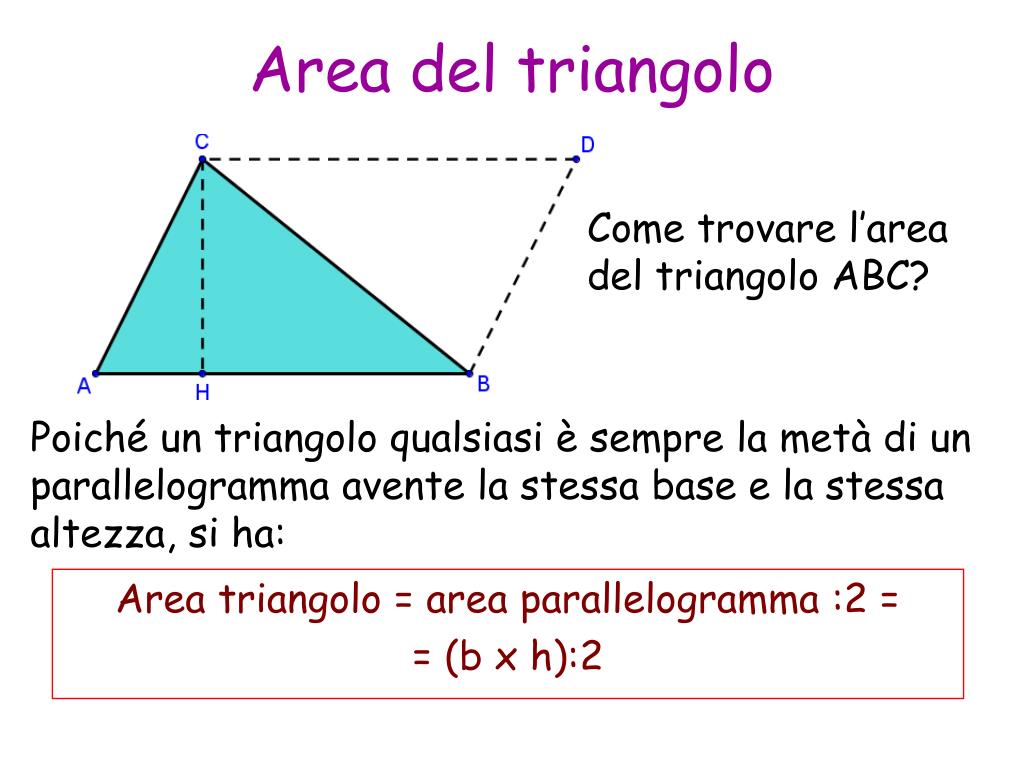
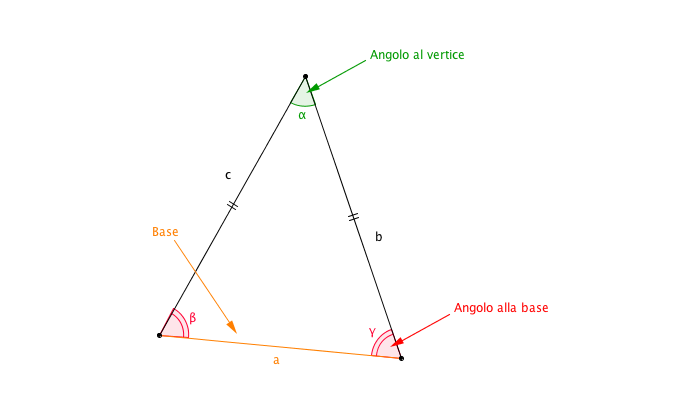
Il calcolo dell'area di un triangolo, in generale, si basa sulla formula: Area = (base * altezza) / 2. Nel caso specifico del triangolo isoscele, questa formula rimane valida, ma è importante capire come determinare la base e, soprattutto, l'altezza. La base è il lato diseguale del triangolo, mentre l'altezza è la perpendicolare che parte dal vertice opposto alla base e arriva fino al punto medio della base stessa. Quest'ultima proprietà è dovuta alla simmetria del triangolo isoscele.
Perché è importante comprendere il calcolo dell'area?
La comprensione del calcolo dell'area del triangolo isoscele è cruciale per gli studenti per diversi motivi. Innanzitutto, rafforza i concetti di base della geometria, come la relazione tra lati, angoli e area. In secondo luogo, prepara gli studenti a risolvere problemi più complessi in geometria e trigonometria. Infine, l'abilità di calcolare l'area ha applicazioni pratiche in diversi campi, dall'architettura all'ingegneria.
"La geometria non è solo misurare la terra; è capire le forme e le loro relazioni. Calcolare l'area è una competenza fondamentale per navigare nel mondo che ci circonda." - Maria Montessori
Metodi per Calcolare l'Area
Esistono diversi metodi per calcolare l'area di un triangolo isoscele, a seconda delle informazioni disponibili:
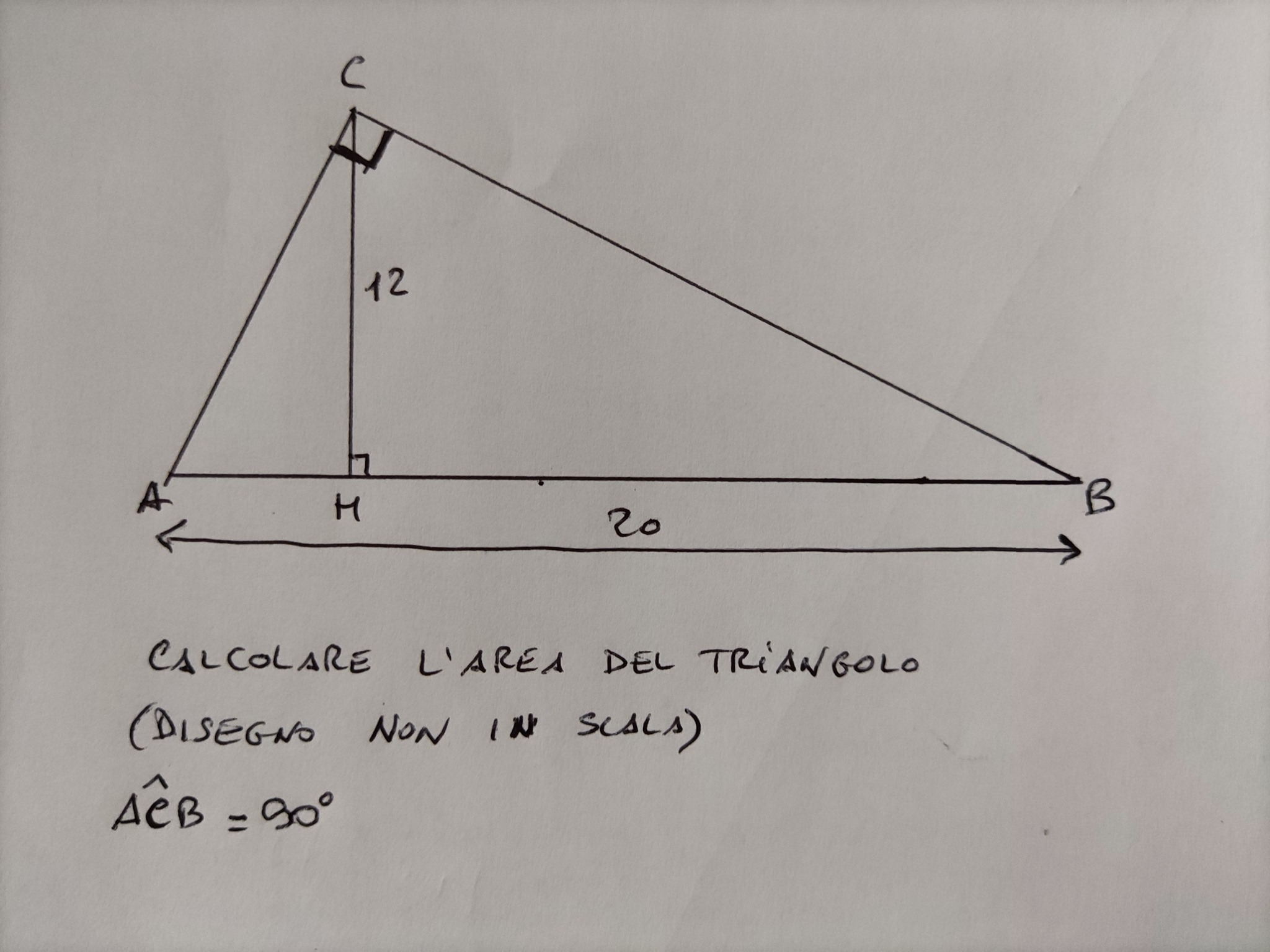
- Metodo 1: Base e Altezza Conosciute: Se conosciamo la lunghezza della base (b) e dell'altezza (h), possiamo applicare direttamente la formula: Area = (b * h) / 2.
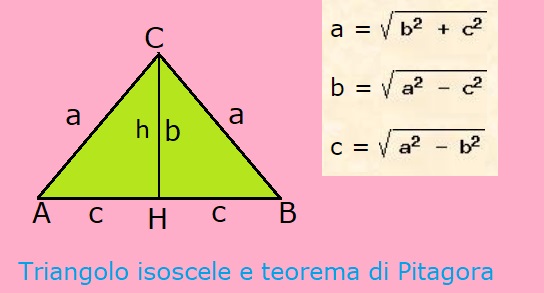
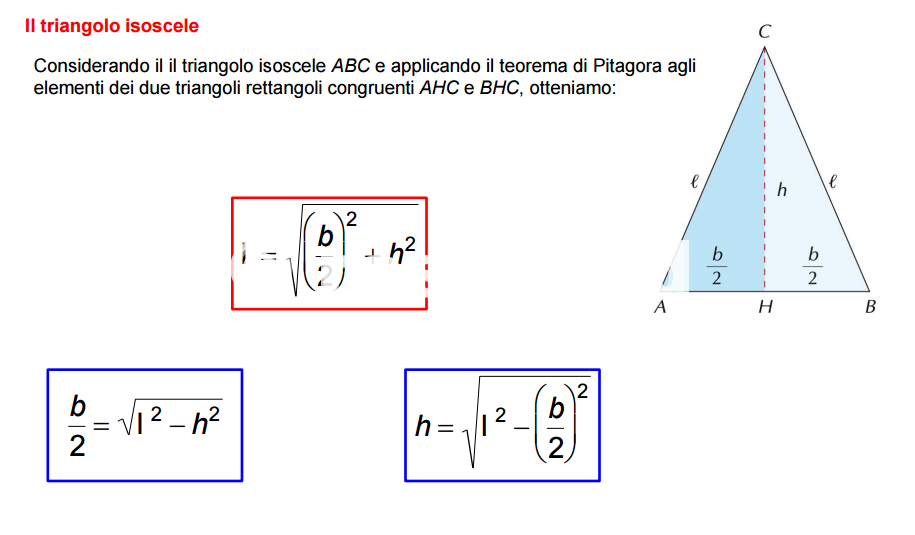
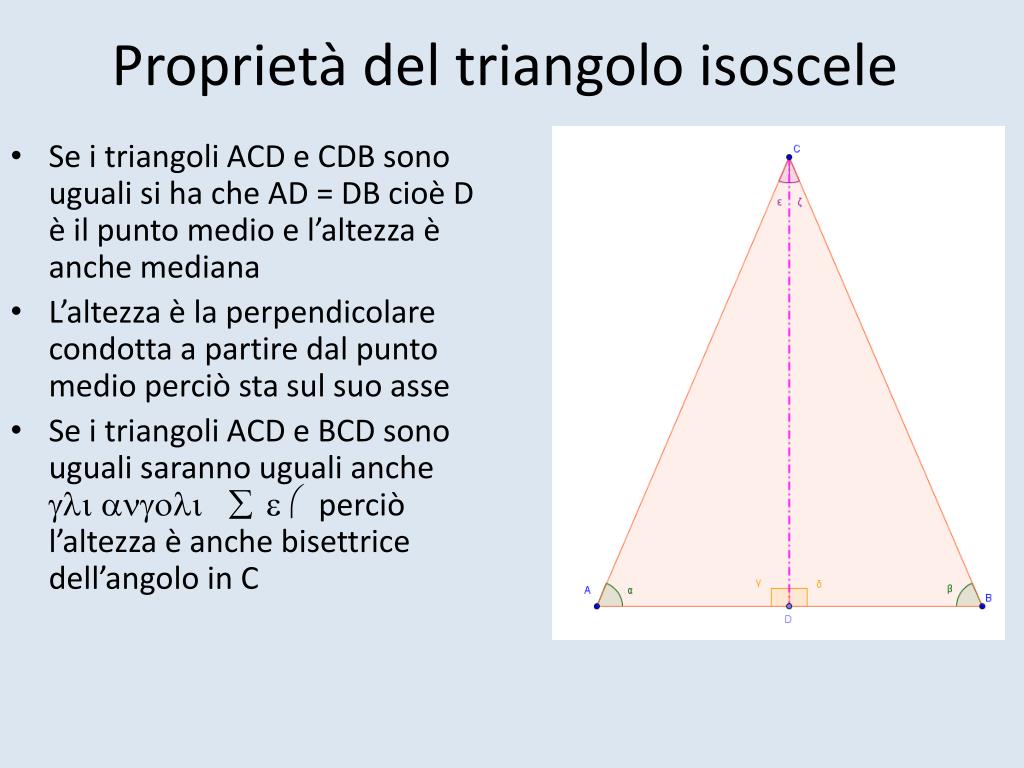
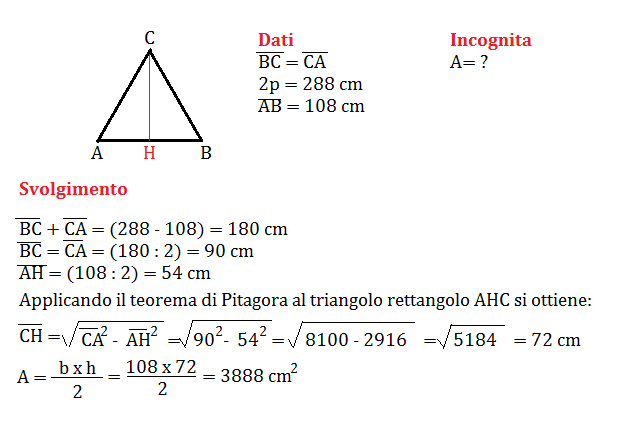
- Metodo 2: Conoscendo i Lati Uguali e la Base: Se conosciamo la lunghezza dei due lati uguali (l) e della base (b), possiamo utilizzare il teorema di Pitagora per calcolare l'altezza. L'altezza divide la base in due segmenti uguali di lunghezza b/2. Quindi, l'altezza (h) sarà: h = √(l² - (b/2)²). Una volta calcolata l'altezza, possiamo applicare la formula dell'area.
- Metodo 3: Conoscendo un Lato Uguale e un Angolo: Se conosciamo la lunghezza di un lato uguale (l) e l'angolo al vertice (α), possiamo utilizzare la trigonometria per calcolare l'altezza. L'altezza sarà: h = l * cos(α/2). Dopodiché, per trovare la base possiamo fare: b = 2 * l * sin(α/2). Infine calcoliamo l'area con la formula (b * h) / 2.
Applicazioni Pratiche
Le applicazioni del calcolo dell'area di un triangolo isoscele sono molteplici. A scuola, gli studenti possono incontrare questo concetto in problemi di geometria, trigonometria e calcolo. Nella vita quotidiana, può essere utile per calcolare la superficie di un tetto a falda, per progettare un giardino con aiuole triangolari, o per stimare la quantità di materiale necessario per costruire una struttura triangolare. Immaginate di dover costruire una mensola triangolare: sapere come calcolare l'area vi permette di determinare quanta vernice vi serve per dipingerla!
Un altro esempio pratico riguarda la progettazione di loghi. Molti loghi aziendali incorporano forme geometriche, inclusi i triangoli isosceli. Comprendere come calcolare l'area permette ai designer di manipolare le forme e le dimensioni per creare un design esteticamente gradevole ed efficiente in termini di utilizzo dei materiali.
In conclusione, il calcolo dell'area di un triangolo isoscele è una competenza fondamentale che si basa su concetti geometrici di base e trova applicazioni in una vasta gamma di contesti. Padroneggiare questa abilità è un passo importante per sviluppare una solida comprensione della geometria e delle sue applicazioni pratiche.