Come Si Calcola L Area Di Un Parallelogramma

Capita a tutti, prima o poi, di trovarsi di fronte a un parallelogramma. Magari dobbiamo calcolare la superficie di un'aiuola nel nostro giardino che ha proprio quella forma, oppure ci serve per un progetto di bricolage. L'importante è non farsi prendere dal panico! Calcolare l'area di un parallelogramma è molto più semplice di quanto possa sembrare. In questo articolo, esploreremo passo dopo passo come farlo, rendendo il processo chiaro e accessibile a tutti.

Cos'è un Parallelogramma?

Prima di iniziare con i calcoli, è fondamentale capire cosa intendiamo per parallelogramma. Un parallelogramma è un quadrilatero (una figura con quattro lati) che ha le seguenti caratteristiche:

I lati opposti sono paralleli (non si incontrano mai, anche se estesi all'infinito).
I lati opposti sono congruenti (hanno la stessa lunghezza).

Esempi comuni di parallelogrammi includono il rettangolo, il quadrato e il rombo. Quindi, se sapete già come calcolare l'area di queste figure, siete già a buon punto!

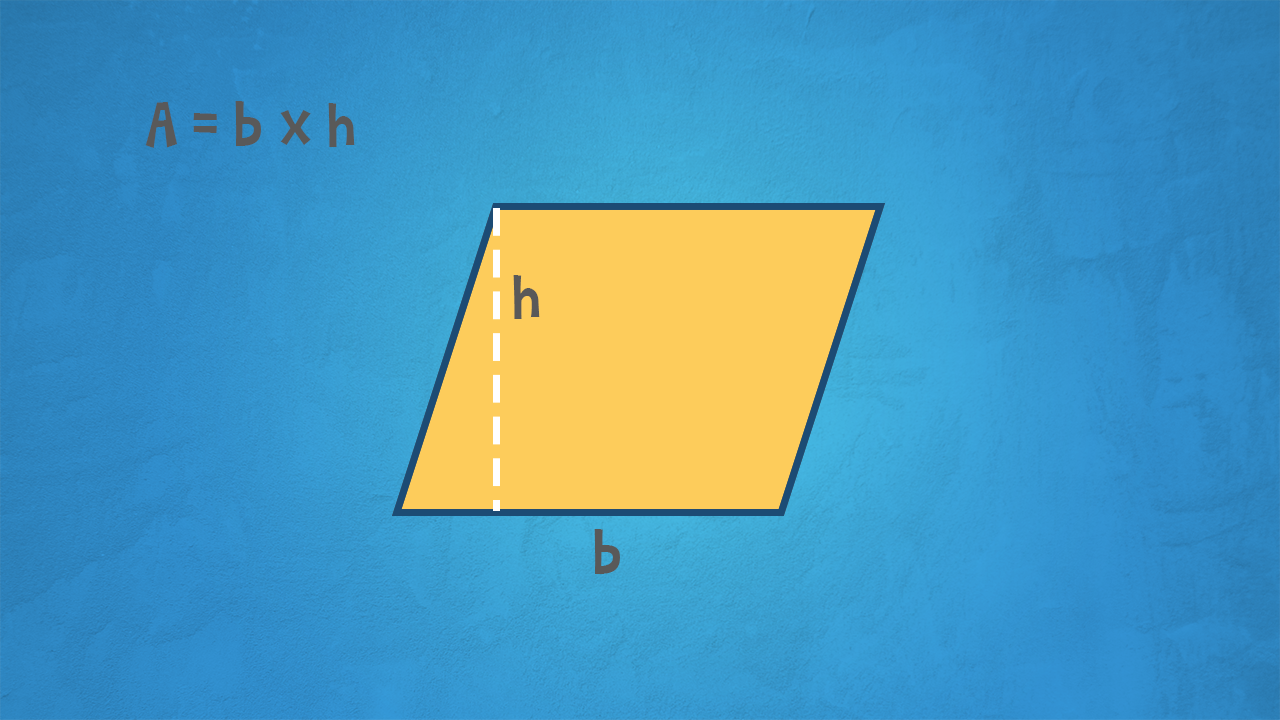
La Formula Magica: Base per Altezza

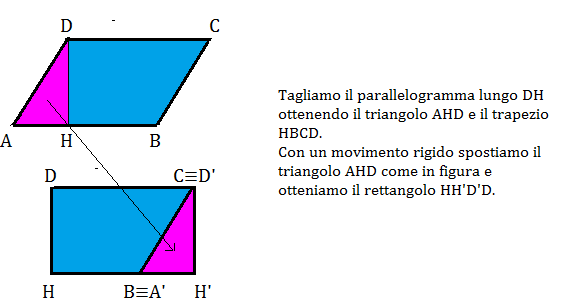
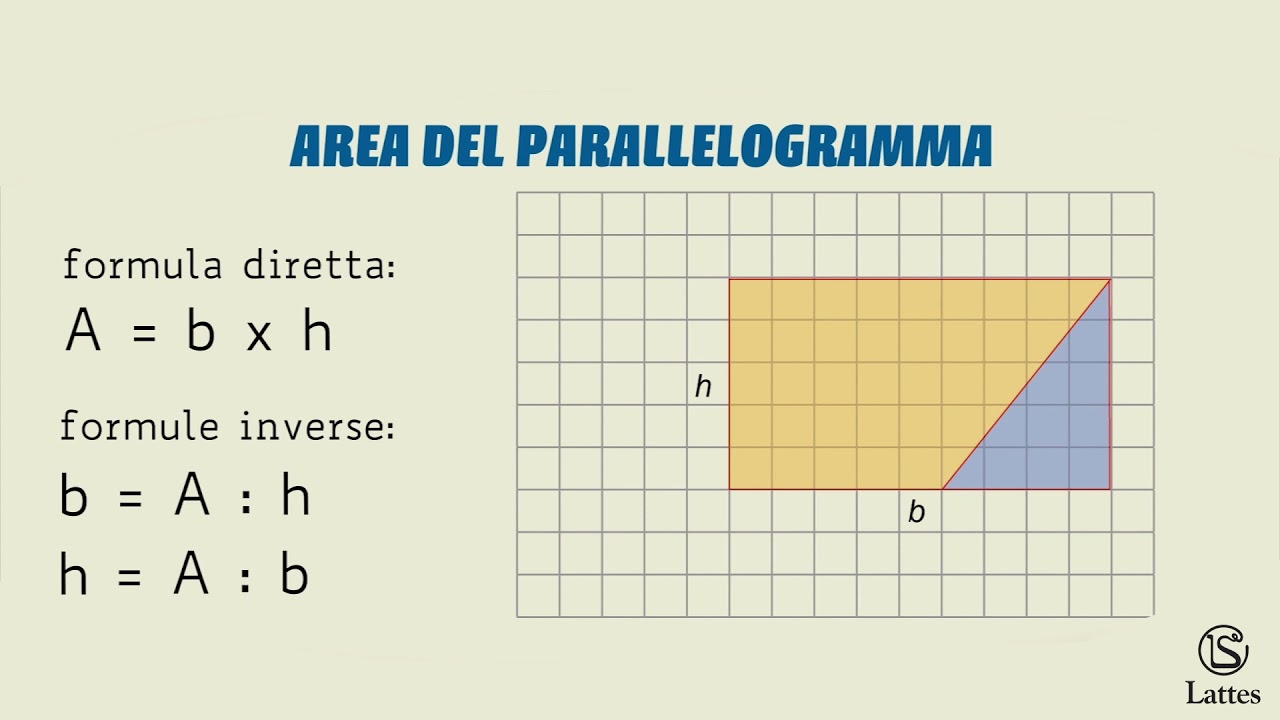
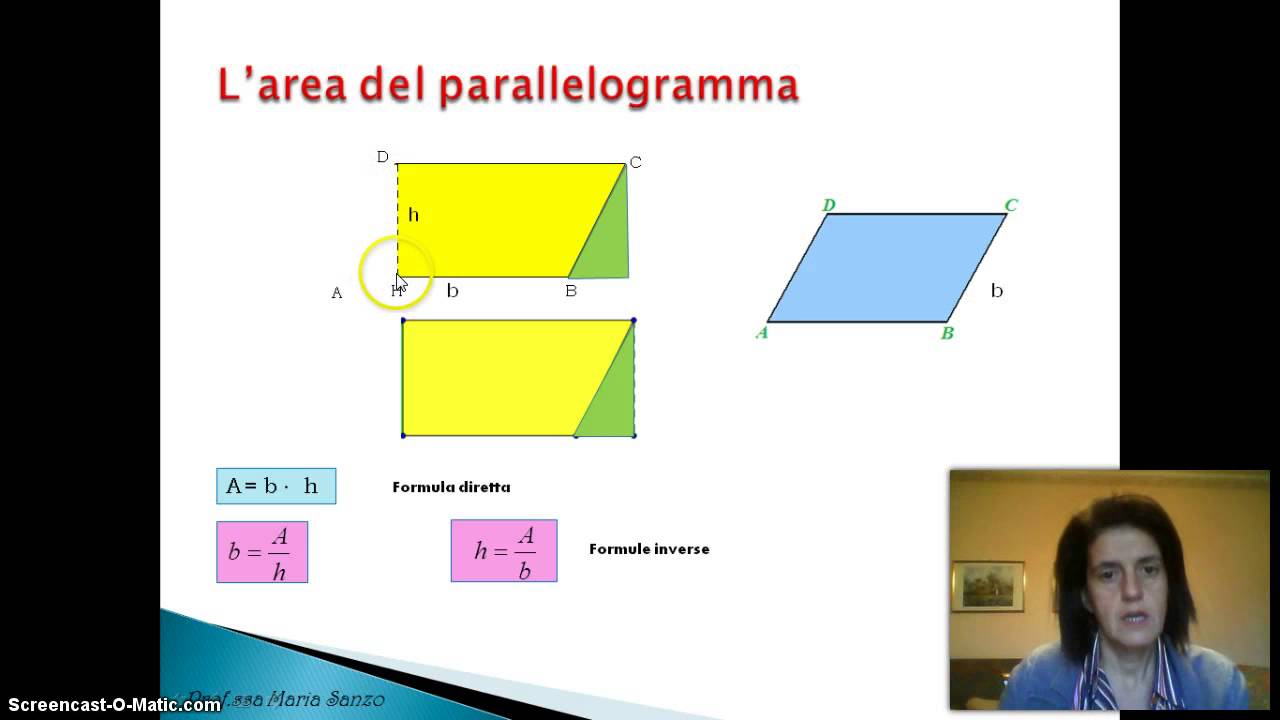
La formula per calcolare l'area di un parallelogramma è sorprendentemente semplice: è base per altezza. Sì, avete capito bene! Ma cosa intendiamo esattamente con "base" e "altezza"?

Definizione di Base e Altezza

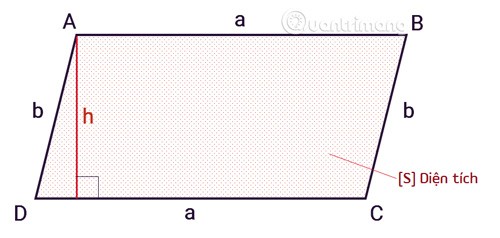
Base: La base è uno qualsiasi dei lati del parallelogramma. Di solito, scegliamo il lato inferiore come base, ma in realtà possiamo scegliere qualsiasi lato.
Altezza: L'altezza è la distanza perpendicolare tra la base e il lato opposto (che è parallelo alla base). Attenzione! L'altezza non è la lunghezza di uno dei lati obliqui del parallelogramma. È una linea retta che forma un angolo di 90 gradi con la base.

Immaginate un rettangolo "spinto" di lato. La base rimane la stessa, ma l'altezza cambia. L'area rimane comunque base per altezza.

Come Trovare l'Altezza

A volte, l'altezza è già fornita nel problema. Altre volte, dovrete calcolarla. Ci sono diversi modi per farlo:

Se conoscete l'angolo e un lato obliquo: Potete utilizzare la trigonometria (seno dell'angolo = altezza / lato obliquo). Quindi, altezza = lato obliquo * seno(angolo).
Se conoscete l'area e la base: Potete semplicemente dividere l'area per la base per trovare l'altezza (altezza = area / base).
Utilizzando il teorema di Pitagora: Se avete un triangolo rettangolo formato dall'altezza, da un segmento della base e da un lato obliquo, potete usare il teorema di Pitagora (a² + b² = c²) per trovare l'altezza.

Esempio Pratico

Supponiamo di avere un parallelogramma con una base di 10 cm e un'altezza di 5 cm. Qual è la sua area?

Usando la formula: Area = base * altezza = 10 cm * 5 cm = 50 cm². Quindi, l'area del parallelogramma è di 50 centimetri quadrati.

Un Esempio Più Complesso

Immaginiamo ora uno scenario più impegnativo. Avete un parallelogramma con una base di 12 cm e un lato obliquo di 8 cm. L'angolo tra la base e il lato obliquo è di 30 gradi. Come calcolate l'area?

Calcolate l'altezza: Usiamo la trigonometria. altezza = lato obliquo * seno(angolo) = 8 cm * seno(30°) = 8 cm * 0.5 = 4 cm.
Calcolate l'area: Area = base * altezza = 12 cm * 4 cm = 48 cm².

Quindi, l'area di questo parallelogramma è di 48 centimetri quadrati.

Parallelogrammi Speciali: Rettangoli, Quadrati e Rombi

Come abbiamo detto prima, rettangoli, quadrati e rombi sono casi speciali di parallelogrammi. Questo significa che la formula base per altezza funziona anche per loro!

Rettangolo: In un rettangolo, l'altezza è semplicemente la lunghezza dell'altro lato (il lato perpendicolare alla base).
Quadrato: In un quadrato, tutti i lati sono uguali. Quindi, l'area è lato * lato (o lato al quadrato).
Rombo: Calcolare l'area di un rombo usando base per altezza è possibile, ma spesso è più semplice usare la formula: (diagonale maggiore * diagonale minore) / 2.

Errori Comuni da Evitare

Ecco alcuni errori comuni che le persone commettono quando calcolano l'area di un parallelogramma:

Confondere l'altezza con il lato obliquo: Ricordate, l'altezza è la distanza perpendicolare tra la base e il lato opposto.
Usare unità di misura diverse: Assicuratevi che la base e l'altezza siano misurate nella stessa unità di misura (ad esempio, centimetri o metri). Se non lo sono, convertitele prima di fare il calcolo.
Dimenticare le unità di misura nell'area: L'area è misurata in unità quadrate (ad esempio, cm² o m²).

Perché è Importante Sapere Come Calcolare l'Area di un Parallelogramma?

Potreste chiedervi: "Quando mai mi servirà sapere come calcolare l'area di un parallelogramma nella vita reale?". La risposta è: più spesso di quanto pensiate! Ecco alcuni esempi:

Architettura e Ingegneria: Gli architetti e gli ingegneri devono calcolare le aree di diverse superfici per progettare edifici e strutture.
Giardinaggio e Paesaggistica: I giardinieri e i paesaggisti devono calcolare le aree per pianificare aiuole, prati e altre aree verdi.
Bricolage e Fai da Te: Se state costruendo un mobile, realizzando un progetto di cucito o dipingendo una parete, avrete bisogno di calcolare le aree per stimare i materiali necessari.
Matematica e Fisica: La comprensione delle aree è fondamentale per concetti più avanzati in matematica e fisica.

Contro-argomentazioni: "Non userò mai questa formula!"

Alcuni potrebbero dire: "Non ho intenzione di diventare un architetto o un ingegnere. Non userò mai questa formula nella mia vita!". Anche se questo può essere vero per alcune persone, imparare a risolvere problemi matematici come questo sviluppa il pensiero critico e le capacità di problem solving, che sono preziose in qualsiasi campo della vita. Inoltre, non si sa mai quando potrebbe tornare utile! Magari un giorno avrete bisogno di calcolare la quantità di vernice necessaria per dipingere una parete con una forma insolita.

In Sintesi: Semplice, Efficace, Utile

Calcolare l'area di un parallelogramma è un'abilità semplice, efficace e utile. Con la formula base per altezza, potete facilmente trovare l'area di qualsiasi parallelogramma, a patto che conosciate la base e l'altezza. Ricordate di prestare attenzione alle unità di misura e di evitare gli errori comuni. E non dimenticate che questa abilità può tornarvi utile in molte situazioni diverse nella vita reale.

Ora tocca a voi!

Avete mai incontrato un parallelogramma nella vostra vita di tutti i giorni? Come avete usato le vostre conoscenze per risolvere un problema pratico? Prendetevi un momento per riflettere su questo e, magari, provate a risolvere qualche esercizio online per consolidare le vostre nuove competenze. Che tipo di progetto potresti intraprendere ora che sai calcolare l'area di un parallelogramma?