Come Si Calcola L Area Del Triangolo Scaleno
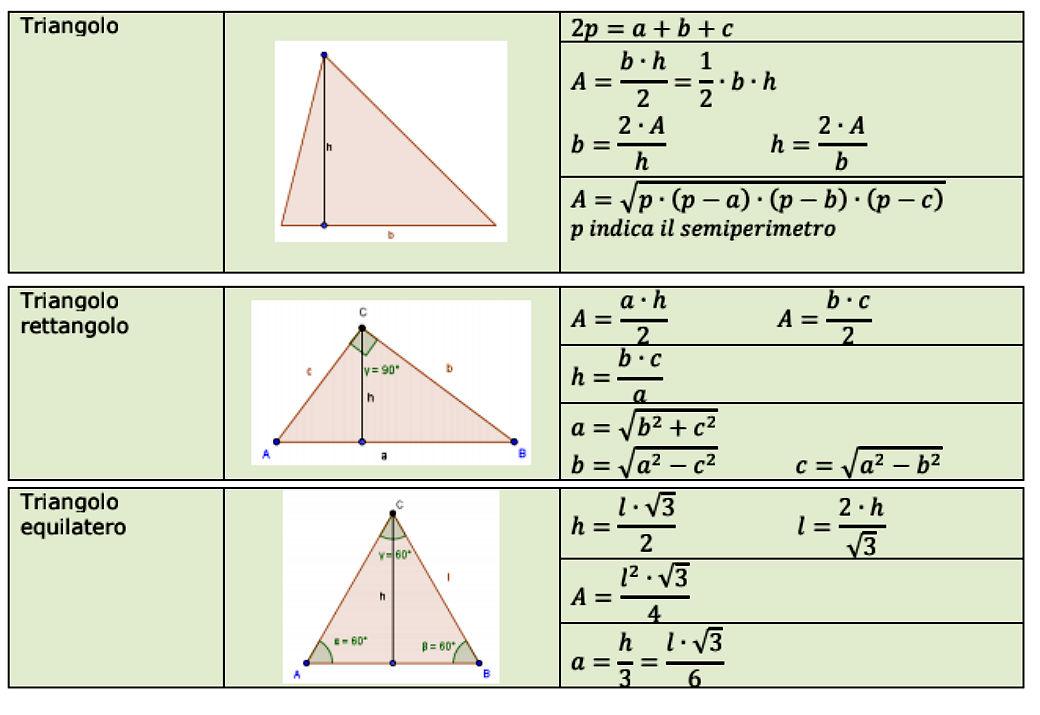
Il triangolo scaleno, con i suoi tre lati di lunghezza diversa, rappresenta una figura geometrica fondamentale, presente in innumerevoli contesti, dall'architettura all'ingegneria, fino all'arte e al design. Comprendere come calcolarne l'area è quindi una competenza preziosa. A differenza di triangoli più semplici come quelli equilateri o rettangoli, non possiamo affidarci a formule immediate. Tuttavia, esistono diversi metodi per calcolare l'area di un triangolo scaleno, ciascuno con i suoi vantaggi e le sue applicazioni. Questa guida esplorerà in dettaglio le tecniche principali, fornendo una comprensione approfondita e pratica.
Diversi Metodi per Calcolare l'Area
Calcolare l'area di un triangolo scaleno richiede un approccio più sofisticato rispetto a quello utilizzato per altri tipi di triangoli. La chiave sta nell'adattare la formula al tipo di informazioni che abbiamo a disposizione. Esploreremo le formule più comuni, spiegandone le basi e le applicazioni.
La Formula di Erone: Quando Conosciamo i Tre Lati
La formula di Erone è uno strumento potente quando conosciamo la lunghezza di tutti e tre i lati del triangolo scaleno. Questa formula, elegante e precisa, ci permette di determinare l'area senza la necessità di conoscere l'altezza o gli angoli interni. Il punto di partenza è il semiperimetro, indicato con 's', calcolato come la metà della somma dei tre lati: s = (a + b + c) / 2, dove a, b e c sono le lunghezze dei lati.
Una volta calcolato il semiperimetro, l'area (A) può essere determinata utilizzando la seguente formula: A = √[s(s - a)(s - b)(s - c)]
Esempio: Supponiamo di avere un triangolo scaleno con lati di lunghezza a = 5 cm, b = 7 cm, e c = 10 cm. * Calcoliamo il semiperimetro: s = (5 + 7 + 10) / 2 = 11 cm * Applichiamo la formula di Erone: A = √[11(11 - 5)(11 - 7)(11 - 10)] = √[11 * 6 * 4 * 1] = √264 ≈ 16.25 cm²
La formula di Erone è particolarmente utile quando non si ha accesso ad altre informazioni sul triangolo oltre alle lunghezze dei suoi lati. È una soluzione elegante e sempre valida, se i dati forniti sono corretti.
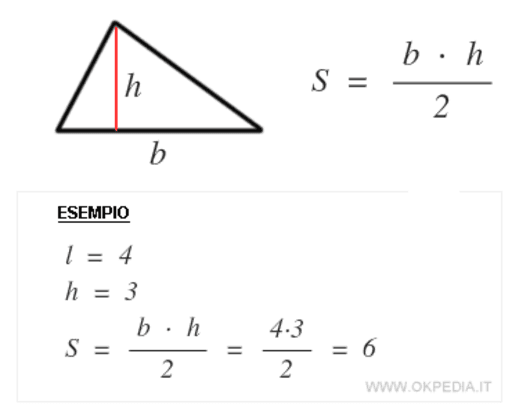
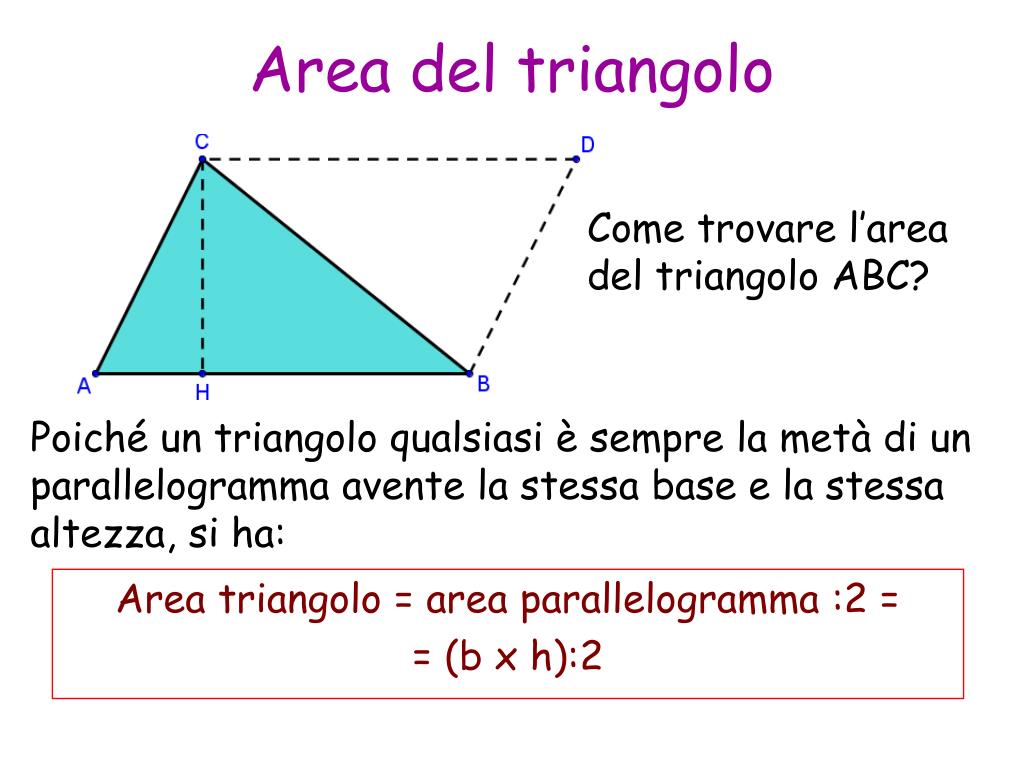
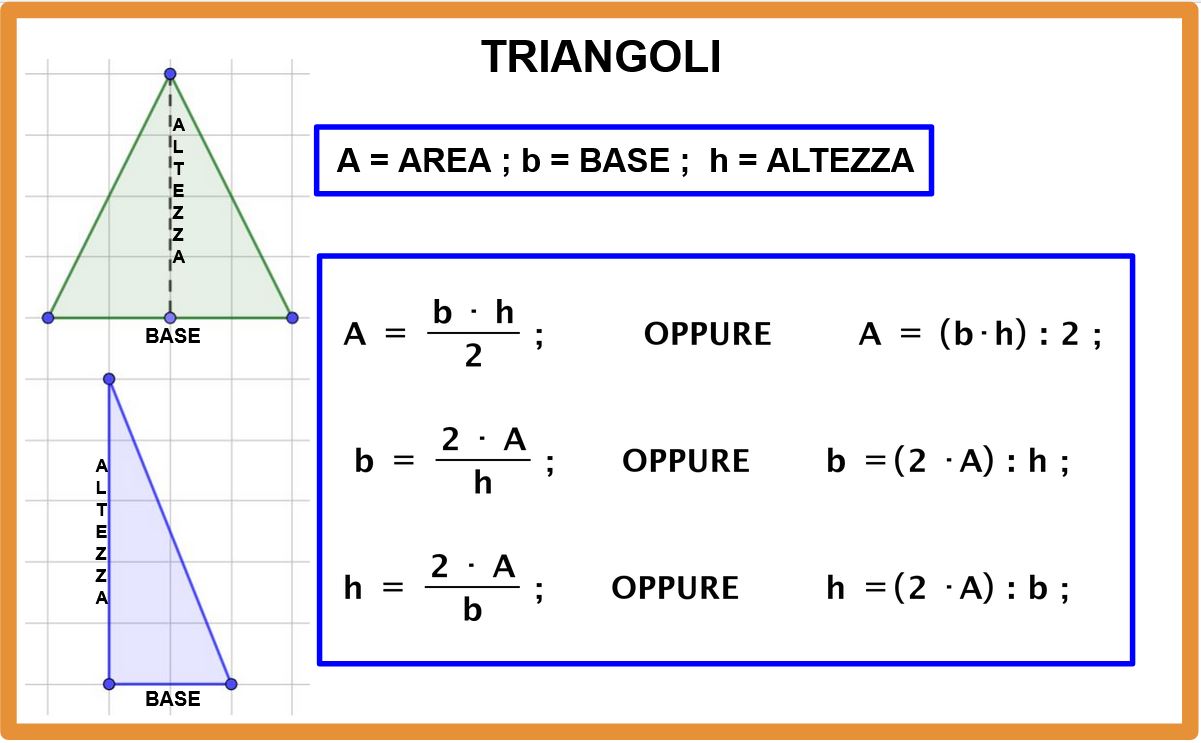
Base e Altezza: Il Metodo Classico
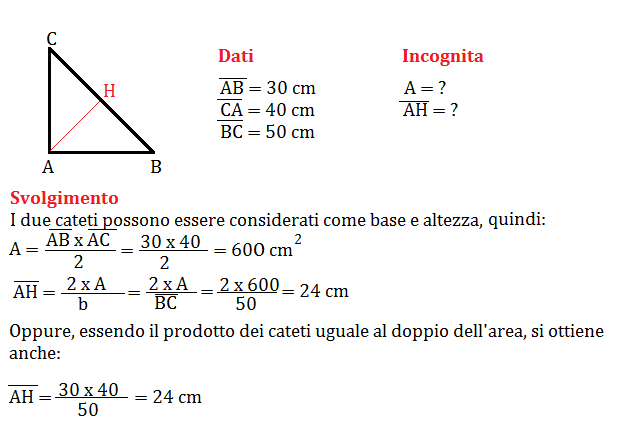
Il metodo più intuitivo per calcolare l'area di un triangolo, valido per qualsiasi tipo di triangolo (incluso quello scaleno), si basa sulla conoscenza della base e dell'altezza. La formula è semplice: A = (base * altezza) / 2.
Tuttavia, nel caso del triangolo scaleno, determinare l'altezza può essere un po' più complesso. L'altezza è la distanza perpendicolare dalla base al vertice opposto. A seconda del problema, potrebbe essere necessario calcolare l'altezza utilizzando il teorema di Pitagora o le funzioni trigonometriche (seno, coseno, tangente) se si conoscono gli angoli interni e la lunghezza di almeno un lato.
Esempio: Immaginiamo un triangolo scaleno con una base di 8 cm e un'altezza corrispondente di 6 cm. L'area sarebbe: A = (8 * 6) / 2 = 24 cm².
Questo metodo è diretto e facile da applicare, ma richiede di conoscere (o di poter calcolare facilmente) l'altezza relativa a una delle basi.
Utilizzo della Trigonometria: Quando Conosciamo Due Lati e l'Angolo Compreso
Se conosciamo la lunghezza di due lati di un triangolo scaleno (ad esempio, a e b) e l'angolo compreso tra di essi (γ), possiamo utilizzare la trigonometria per calcolare l'area. La formula è: A = (1/2) * a * b * sin(γ).
Questa formula si basa sulla relazione tra il seno di un angolo e l'altezza del triangolo. In pratica, il seno dell'angolo compreso, moltiplicato per uno dei lati, ci fornisce un'informazione direttamente proporzionale all'altezza relativa all'altro lato.
Esempio: Supponiamo di avere un triangolo scaleno con lati a = 6 cm, b = 9 cm, e un angolo γ di 40 gradi tra di essi. * Calcoliamo il seno di 40 gradi: sin(40°) ≈ 0.643 * Applichiamo la formula: A = (1/2) * 6 * 9 * 0.643 ≈ 17.36 cm²
Questa formula è particolarmente utile quando ci vengono forniti due lati e l'angolo che formano. È un metodo efficiente e preciso, a condizione di avere una calcolatrice scientifica per calcolare il seno dell'angolo.
Coordinate dei Vertici: Geometria Analitica
Se conosciamo le coordinate dei tre vertici del triangolo scaleno in un piano cartesiano (ad esempio, A(x1, y1), B(x2, y2), e C(x3, y3)), possiamo calcolare l'area utilizzando una formula derivata dalla geometria analitica. Questa formula è basata sul determinante di una matrice:
A = (1/2) |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|
Il valore assoluto assicura che l'area sia sempre positiva. Questa formula è una potente applicazione della geometria analitica e offre un metodo diretto per calcolare l'area quando si hanno le coordinate dei vertici.
Esempio: Consideriamo un triangolo scaleno con vertici A(1, 2), B(4, 5), e C(6, 1). * Applichiamo la formula: A = (1/2) |1(5 - 1) + 4(1 - 2) + 6(2 - 5)| = (1/2) |4 - 4 - 18| = (1/2) |-18| = 9 unità di area.
Questa formula è preziosa in contesti in cui il triangolo è definito in un sistema di coordinate, come nella grafica computerizzata o nella progettazione assistita da computer (CAD).
Esempi Reali e Applicazioni Pratiche
La capacità di calcolare l'area di un triangolo scaleno trova applicazione in una vasta gamma di settori. Eccone alcuni esempi:
- Architettura e Ingegneria Civile: Nel progettare tetti, ponti o altre strutture, è fondamentale calcolare l'area di superfici triangolari irregolari per determinare la quantità di materiale necessario e la distribuzione dei carichi.
- Geodesia e Cartografia: Nel rilevamento del territorio e nella creazione di mappe, i triangoli scaleni sono spesso utilizzati per approssimare forme complesse e calcolare aree di terreni.
- Design e Arte: Molti oggetti di design e opere d'arte incorporano forme triangolari scalene. La capacità di calcolare l'area aiuta a determinare le proporzioni e l'estetica complessiva.
- Taglio e Confezionamento: Nel taglio di tessuti, legno o altri materiali, conoscere l'area di un triangolo scaleno permette di ottimizzare l'utilizzo del materiale e ridurre gli sprechi.
- Videogiochi e Grafica Computerizzata: I triangoli sono i blocchi fondamentali per la creazione di modelli 3D. Calcolare l'area di un triangolo scaleno è essenziale per il rendering e la manipolazione di oggetti virtuali.
Ad esempio, immagina di dover calcolare la quantità di vernice necessaria per dipingere un muro triangolare. Se conosci le dimensioni dei tre lati del triangolo, puoi utilizzare la formula di Erone per calcolare l'area e, di conseguenza, la quantità di vernice necessaria. Oppure, pensa a un architetto che deve progettare un tetto con una forma triangolare irregolare. Conoscere l'area del triangolo è fondamentale per stimare i costi dei materiali e garantire la stabilità della struttura.
Conclusioni
Calcolare l'area di un triangolo scaleno può sembrare complicato a prima vista, ma come abbiamo visto, esistono diverse formule e metodi a seconda delle informazioni che abbiamo a disposizione. Dalla formula di Erone all'utilizzo della base e dell'altezza, dalla trigonometria alla geometria analitica, ogni approccio offre una soluzione adatta a diverse situazioni.
La chiave per risolvere con successo questi problemi è comprendere le basi della geometria e della trigonometria, e scegliere la formula più appropriata in base ai dati forniti. La pratica è fondamentale: esercitarsi con diversi esempi e problemi aiuterà a consolidare la comprensione e ad acquisire la sicurezza necessaria per affrontare qualsiasi sfida geometrica.
Invitiamo quindi a esplorare ulteriormente questi concetti, a sperimentare con diverse formule e a cercare applicazioni pratiche nel mondo che ci circonda. La geometria è ovunque, e la capacità di comprenderla e manipolarla è un'abilità preziosa in molti campi.