Come Si Calcola L Altezza Di Un Rettangolo

Quante volte ti sei trovato di fronte a un rettangolo, magari durante i compiti di geometria, e ti sei bloccato, chiedendoti: "Come diavolo calcolo l'altezza?". Non sei solo! Molti studenti, genitori che aiutano con i compiti, e persino insegnanti alle prime armi, a volte si sentono persi di fronte a problemi apparentemente semplici come questo. La geometria, a volte, può sembrare un labirinto di formule e regole. Ma non temere! Questa guida è qui per svelare il mistero dell'altezza del rettangolo in modo chiaro, strutturato e, soprattutto, facile da capire.

Cos'è un Rettangolo? Un Ripasso Fondamentale

Prima di tuffarci nei calcoli, ripassiamo velocemente cos'è un rettangolo. Un rettangolo è un quadrilatero (una figura geometrica con quattro lati) con le seguenti caratteristiche:

Quattro angoli retti: Ogni angolo misura esattamente 90 gradi.
Lati opposti uguali e paralleli: I lati opposti sono della stessa lunghezza e non si incontrano mai, nemmeno se prolungati all'infinito.

In un rettangolo, si distinguono due dimensioni principali:

Base (b): Generalmente, il lato orizzontale.
Altezza (h): Generalmente, il lato verticale.

Anche se spesso usiamo "base" e "altezza", è importante capire che in realtà *qualsiasi* dei due lati può essere considerato la base, e l'altro l'altezza. L'importante è che siano i lati perpendicolari (che formano un angolo di 90 gradi) tra loro.

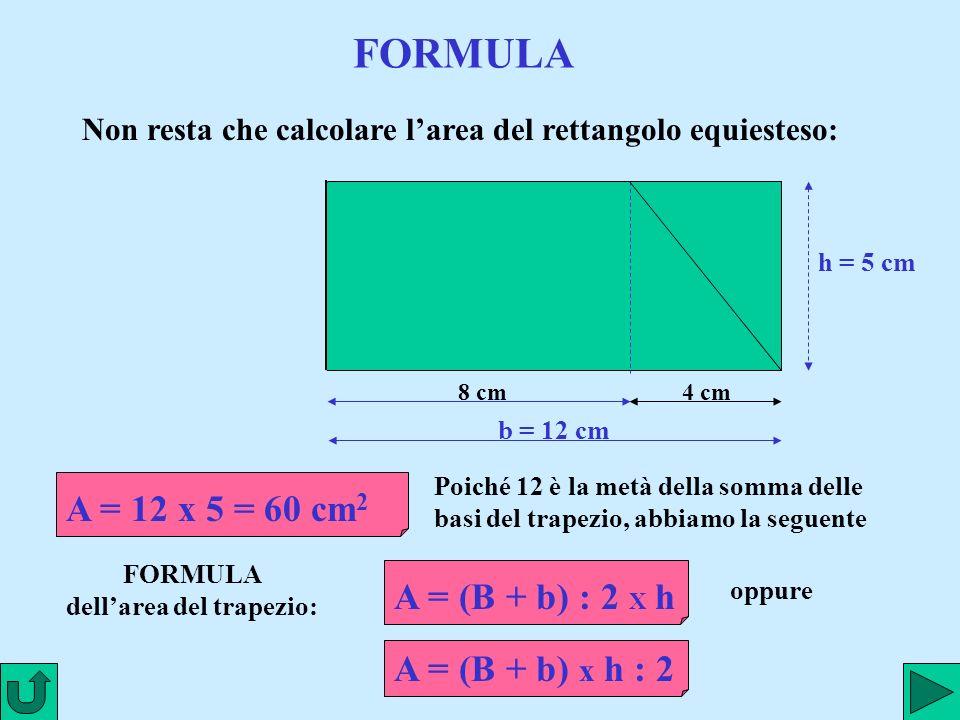
Metodo 1: Conoscendo l'Area e la Base

Questo è il metodo più comune e, probabilmente, il più semplice. Se conosciamo l'area (A) del rettangolo e la sua base (b), possiamo calcolare l'altezza (h) utilizzando la seguente formula:

h = A / b

In parole povere, l'altezza è uguale all'area divisa per la base.

Esempio Pratico

Immagina di avere un rettangolo che rappresenta un prato. Sappiamo che l'area del prato è di 36 metri quadrati (A = 36 m²) e la sua base è di 9 metri (b = 9 m). Vogliamo calcolare l'altezza del prato.

Applicando la formula:

h = 36 m² / 9 m = 4 m

Quindi, l'altezza del prato è di 4 metri.

Esercizio per Casa

Un rettangolo ha un'area di 48 cm² e una base di 8 cm. Calcola la sua altezza.

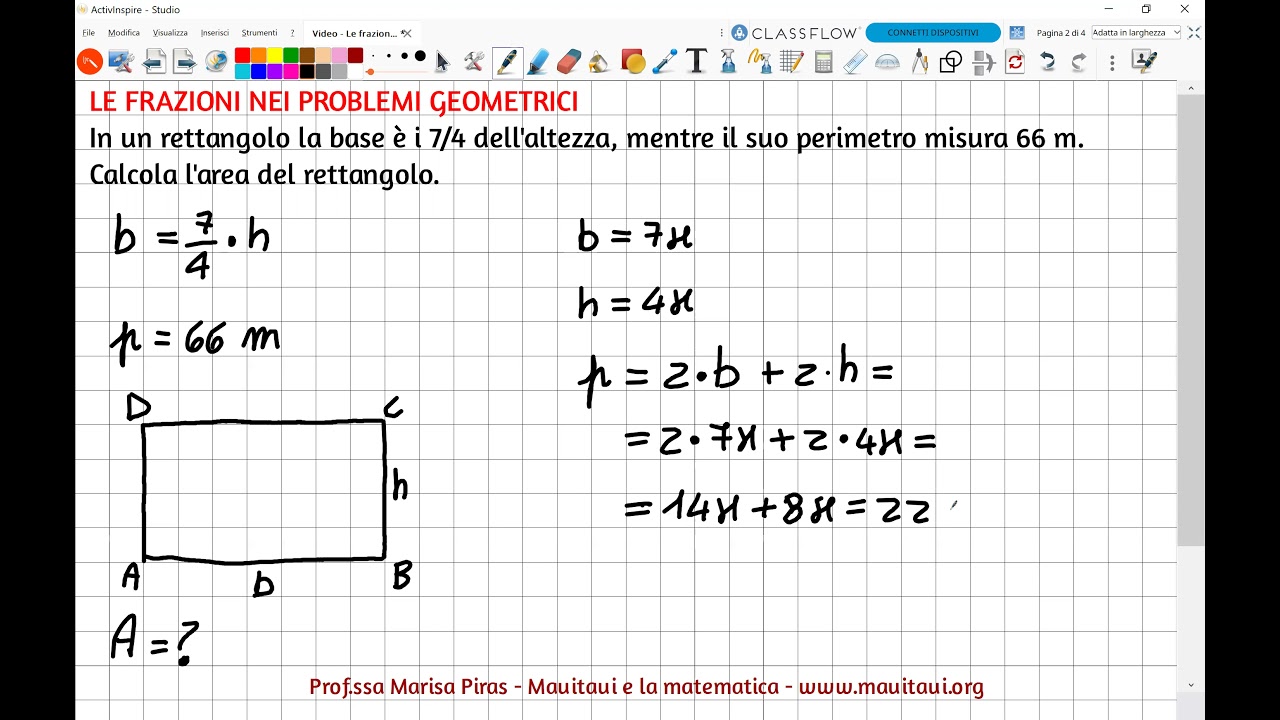
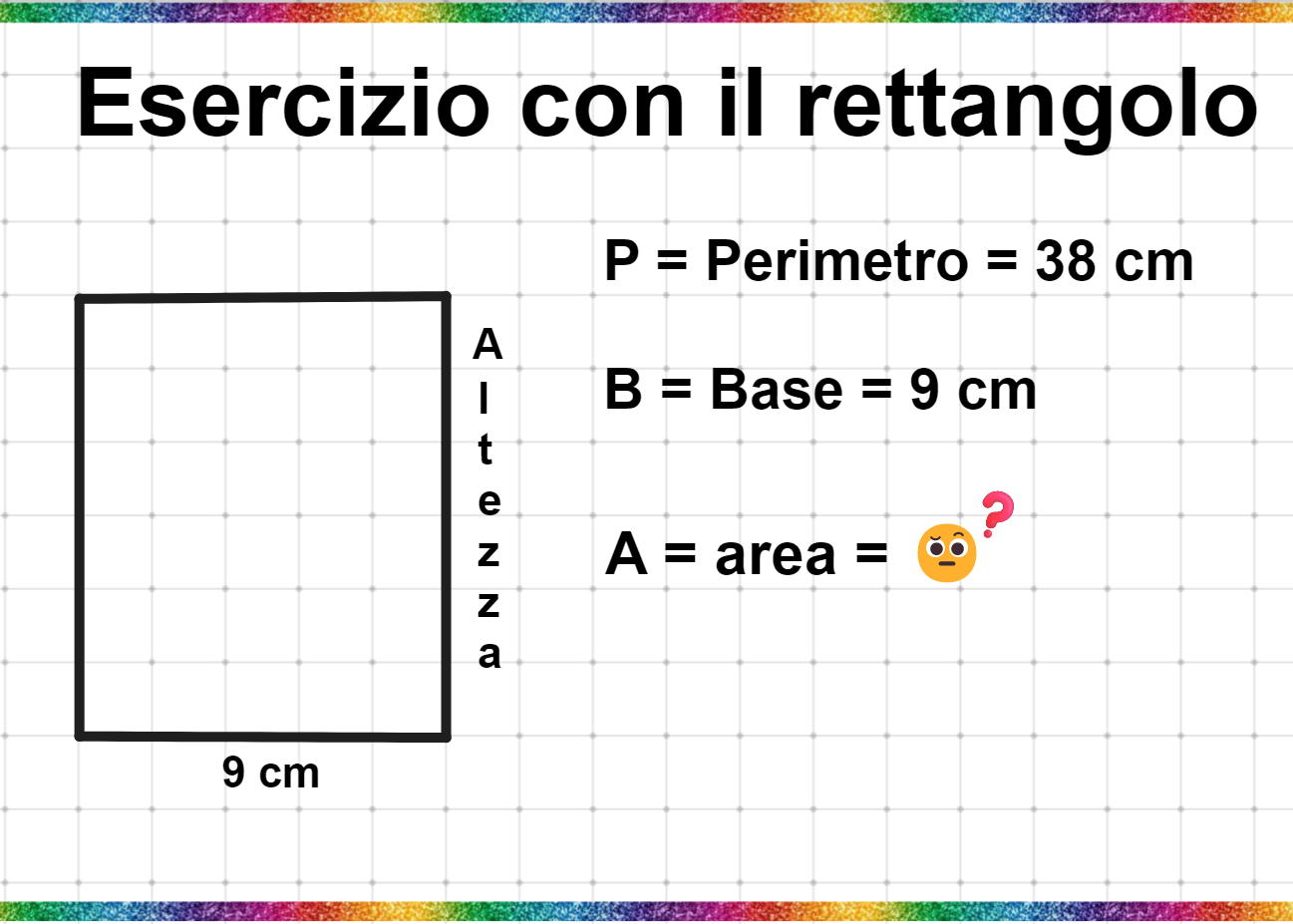
Metodo 2: Conoscendo il Perimetro e la Base

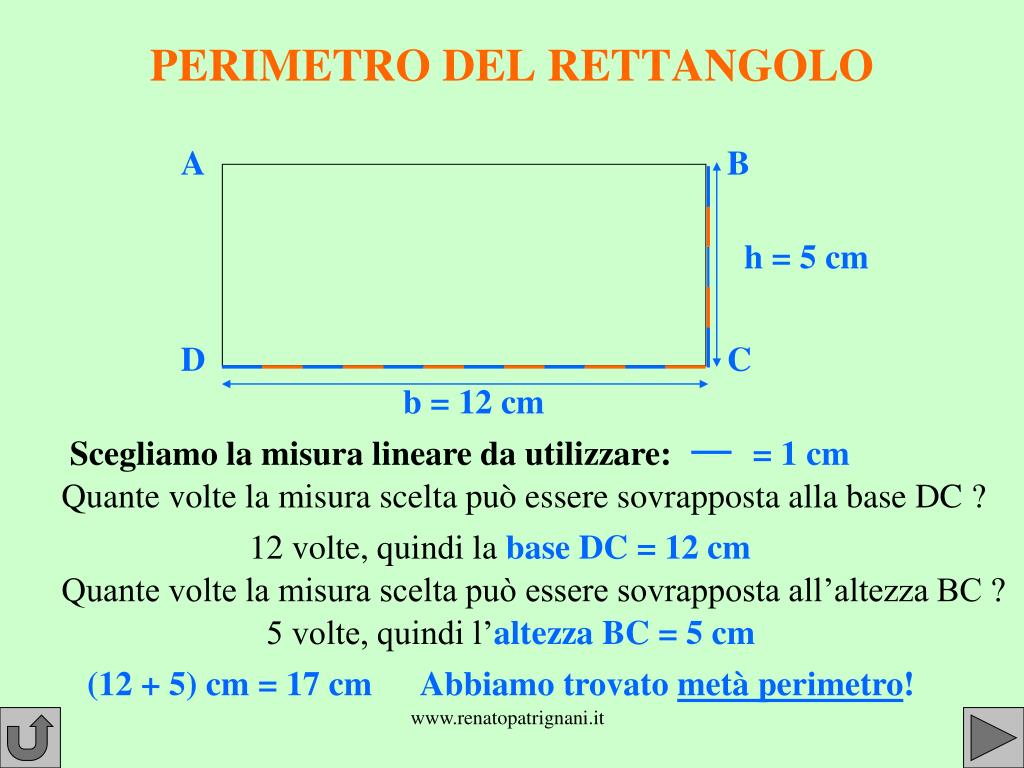
Se invece di conoscere l'area, conosciamo il perimetro (P) del rettangolo e la sua base (b), possiamo calcolare l'altezza (h). Ricordiamo che il perimetro è la somma di tutti i lati del rettangolo.

La formula per il perimetro di un rettangolo è:

P = 2b + 2h

Dobbiamo riorganizzare questa formula per isolare l'altezza (h):

Sottraiamo 2b da entrambi i lati: P - 2b = 2h
Dividiamo entrambi i lati per 2: (P - 2b) / 2 = h

Quindi, la formula per calcolare l'altezza conoscendo il perimetro e la base è:

h = (P - 2b) / 2

Esempio Pratico

Supponiamo di avere un rettangolo che rappresenta una cornice. Sappiamo che il perimetro della cornice è di 50 cm (P = 50 cm) e la sua base è di 15 cm (b = 15 cm). Calcoliamo l'altezza della cornice.

Applicando la formula:

h = (50 cm - 2 * 15 cm) / 2 = (50 cm - 30 cm) / 2 = 20 cm / 2 = 10 cm

Quindi, l'altezza della cornice è di 10 cm.

Esercizio per Casa

Un rettangolo ha un perimetro di 64 metri e una base di 20 metri. Calcola la sua altezza.

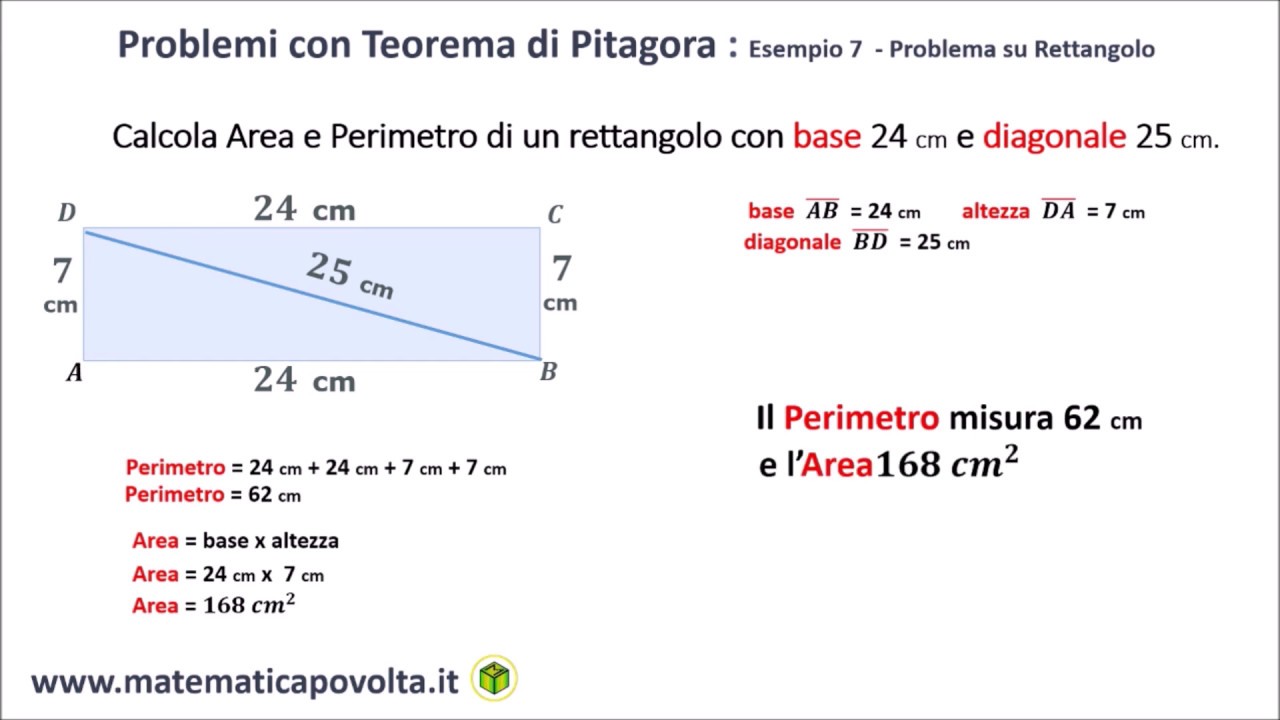
Metodo 3: Utilizzando il Teorema di Pitagora (Se Conosci la Diagonale)

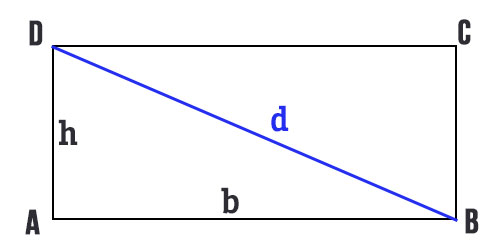
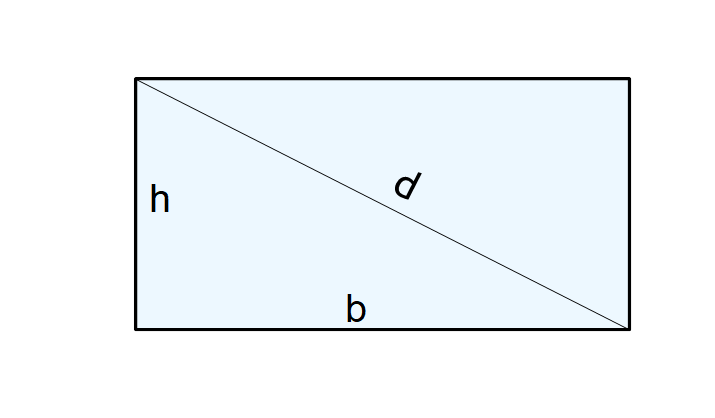
Questo metodo è un po' più avanzato e richiede la conoscenza del Teorema di Pitagora. Se conosciamo la diagonale (d) del rettangolo e la sua base (b), possiamo calcolare l'altezza (h).

Ricordiamo che il Teorema di Pitagora afferma che in un triangolo rettangolo (come quello formato dalla base, dall'altezza e dalla diagonale del rettangolo), il quadrato dell'ipotenusa (il lato opposto all'angolo retto, in questo caso la diagonale) è uguale alla somma dei quadrati degli altri due lati (la base e l'altezza).

In formula:

d² = b² + h²

Dobbiamo riorganizzare questa formula per isolare l'altezza (h):

Sottraiamo b² da entrambi i lati: d² - b² = h²
Calcoliamo la radice quadrata di entrambi i lati: √(d² - b²) = h

Quindi, la formula per calcolare l'altezza conoscendo la diagonale e la base è:

h = √(d² - b²)

Esempio Pratico

Consideriamo un rettangolo che rappresenta uno schermo. Sappiamo che la diagonale dello schermo è di 25 pollici (d = 25 pollici) e la sua base è di 20 pollici (b = 20 pollici). Calcoliamo l'altezza dello schermo.

Applicando la formula:

h = √(25² - 20²) = √(625 - 400) = √225 = 15 pollici

Quindi, l'altezza dello schermo è di 15 pollici.

Esercizio per Casa

Un rettangolo ha una diagonale di 13 cm e una base di 12 cm. Calcola la sua altezza.

Consigli Utili e Errori Comuni da Evitare

Unità di misura: Assicurati che tutte le misure siano nella stessa unità di misura (ad esempio, tutti in centimetri, metri o pollici) prima di effettuare i calcoli.
Confusione tra area e perimetro: Ricorda che l'area è la superficie interna del rettangolo, mentre il perimetro è la lunghezza del suo contorno. Usare la formula sbagliata porterà a risultati errati.
Teorema di Pitagora: Assicurati di identificare correttamente l'ipotenusa (la diagonale) e i cateti (la base e l'altezza) quando utilizzi il Teorema di Pitagora.

Perché è Importante Sapere Calcolare l'Altezza di un Rettangolo?

Potresti chiederti: "Ok, ora so come calcolare l'altezza di un rettangolo, ma a cosa mi serve?". La risposta è: a tantissime cose!

Compiti scolastici: Ovviamente, è fondamentale per superare gli esercizi di geometria e matematica.
Progetti fai-da-te: Quando costruisci qualcosa, ad esempio una mensola o un mobile, conoscere le dimensioni corrette (inclusa l'altezza) è cruciale.
Arredamento: Quando scegli un quadro, uno specchio o qualsiasi altro oggetto da appendere, devi considerare l'altezza disponibile sulla parete.
Architettura e design: Gli architetti e i designer utilizzano costantemente i concetti di base e altezza per progettare edifici, stanze e oggetti.

Secondo alcune ricerche (e anche la semplice osservazione della vita quotidiana!), la comprensione dei concetti geometrici di base, come il calcolo dell'altezza, contribuisce a sviluppare il pensiero logico-matematico e le capacità di problem solving. Una solida base in geometria apre la strada a studi più avanzati in matematica, fisica e ingegneria.

Conclusione: Non Avere Paura della Geometria!

Spero che questa guida ti abbia aiutato a capire meglio come calcolare l'altezza di un rettangolo. Ricorda, la chiave è la pratica. Più esercizi fai, più diventerai bravo e sicuro di te. Non avere paura di fare errori, perché è proprio dagli errori che si impara! E se hai ancora dubbi, non esitare a chiedere aiuto al tuo insegnante, a un amico o a cercare ulteriori risorse online.

La geometria, come la vita, è fatta di forme e dimensioni. Imparare a comprenderle ti aprirà un mondo di possibilità!