Come Si Calcola Il Perimetro Di Base Di Un Prisma

Capita spesso di trovarsi di fronte a figure geometriche complesse e sentirsi un po' smarriti. Uno di questi casi è il prisma, un solido geometrico affascinante ma che, a volte, può sembrare difficile da affrontare. Una delle prime sfide che si presentano è il calcolo del perimetro di base. Non preoccuparti, non sei solo! Molti studenti, professionisti e semplici appassionati di geometria si trovano a dover affrontare questo problema. Questo articolo è pensato proprio per te: per guidarti passo dopo passo attraverso il calcolo del perimetro di base di un prisma, rendendo il processo chiaro e semplice.

Immagina di dover costruire una recinzione attorno alla base di un prisma che hai progettato per un'aiuola nel tuo giardino. Oppure, pensa di dover calcolare la quantità di nastro adesivo necessaria per decorare la base di un prisma di cartone che hai creato per un progetto scolastico. In entrambi i casi, il calcolo del perimetro di base diventa fondamentale. Non si tratta solo di un esercizio teorico; ha implicazioni pratiche che possono influenzare la vita di tutti i giorni.

Cos'è un Prisma?

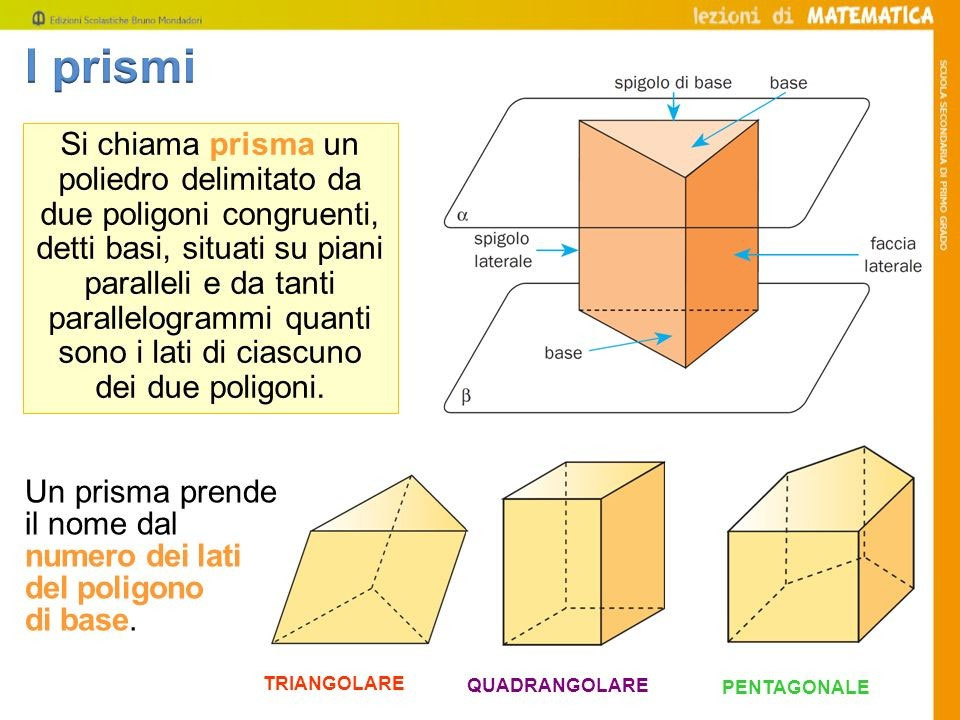
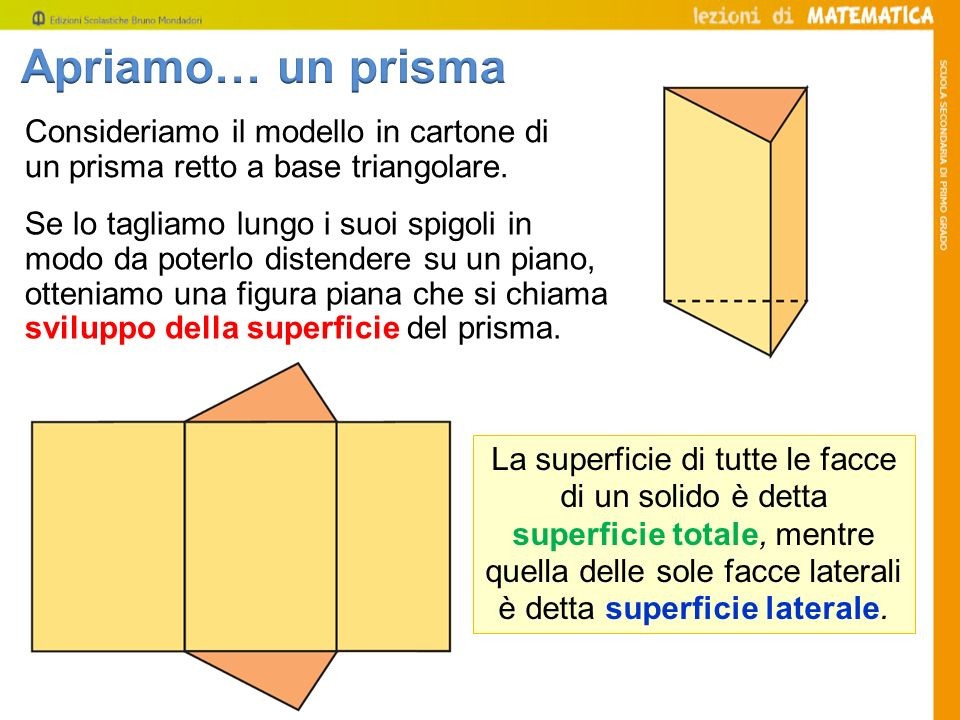
Prima di immergerci nel calcolo del perimetro, ripassiamo rapidamente cos'è un prisma. Un prisma è un solido geometrico delimitato da due poligoni congruenti e paralleli (le basi) e da tanti parallelogrammi quanti sono i lati di ciascuna base (le facce laterali). L'altezza del prisma è la distanza tra le due basi.

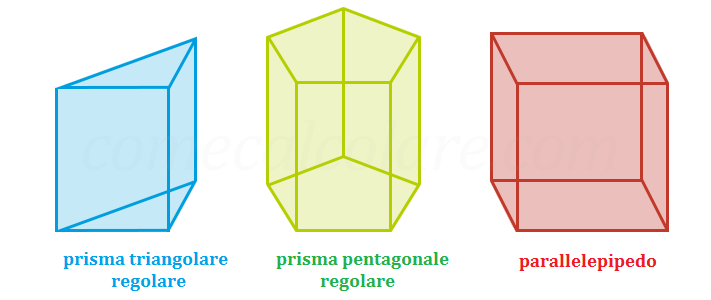
I prismi possono essere classificati in base alla forma delle loro basi: abbiamo prismi triangolari, quadrangolari, pentagonali, esagonali e così via. Ad esempio, un prisma triangolare ha come base un triangolo, mentre un prisma esagonale ha come base un esagono. Questa distinzione è cruciale perché il metodo per calcolare il perimetro di base dipenderà proprio dalla forma della base stessa.

Perché Calcolare il Perimetro di Base?

Il perimetro di base di un prisma è la somma delle lunghezze dei lati del poligono che forma la base. Ma perché è così importante calcolarlo?

Calcolo dell'Area Laterale: Il perimetro di base è un elemento fondamentale per calcolare l'area laterale del prisma. L'area laterale è data dal prodotto tra il perimetro di base e l'altezza del prisma.
Calcolo dell'Area Totale: L'area totale del prisma si ottiene sommando l'area laterale e l'area delle due basi. Anche in questo caso, il perimetro di base è necessario per calcolare l'area laterale e, di conseguenza, l'area totale.
Calcolo del Volume: In alcuni contesti, la conoscenza del perimetro di base può essere utile per dedurre altre proprietà del prisma, anche se non direttamente coinvolto nella formula del volume (che dipende dall'area di base e dall'altezza).
Applicazioni Pratiche: Come accennato all'inizio, il calcolo del perimetro di base ha numerose applicazioni pratiche, dalla costruzione alla progettazione, all'arte e all'artigianato.

Come Calcolare il Perimetro di Base: Approccio Generale

L'approccio generale per calcolare il perimetro di base di un prisma è semplice: sommare le lunghezze di tutti i lati del poligono di base. Tuttavia, la difficoltà può variare a seconda della forma del poligono di base.

Prisma con Base Triangolare

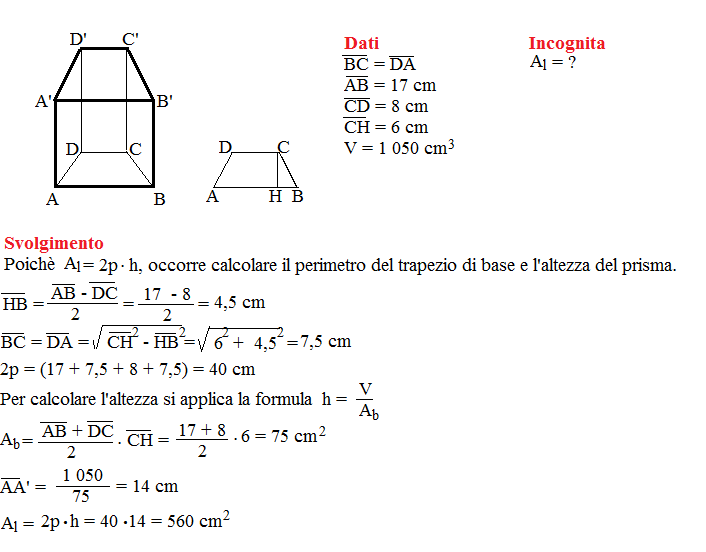
Se la base del prisma è un triangolo, il perimetro si calcola sommando le lunghezze dei tre lati del triangolo: P = a + b + c, dove a, b e c sono le lunghezze dei tre lati.

Triangolo Equilatero: Se il triangolo è equilatero (tutti i lati uguali), il perimetro è semplicemente P = 3a, dove 'a' è la lunghezza di un lato.
Triangolo Isoscele: Se il triangolo è isoscele (due lati uguali), il perimetro è P = 2a + b, dove 'a' è la lunghezza dei due lati uguali e 'b' è la lunghezza del terzo lato.
Triangolo Scaleno: Se il triangolo è scaleno (tutti i lati diversi), è necessario conoscere la lunghezza di ciascun lato per poter calcolare il perimetro.

Prisma con Base Quadrangolare

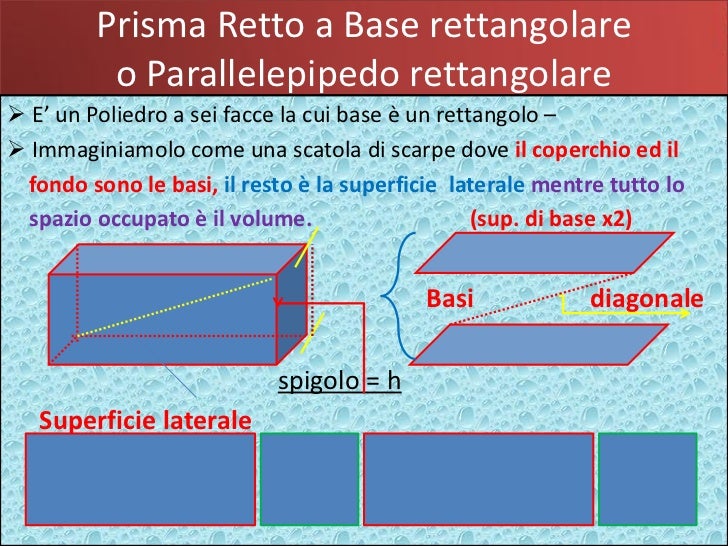
Se la base del prisma è un quadrilatero, il perimetro si calcola sommando le lunghezze dei quattro lati del quadrilatero: P = a + b + c + d, dove a, b, c e d sono le lunghezze dei quattro lati.

Quadrato: Se il quadrilatero è un quadrato (tutti i lati uguali), il perimetro è semplicemente P = 4a, dove 'a' è la lunghezza di un lato.
Rettangolo: Se il quadrilatero è un rettangolo (lati opposti uguali), il perimetro è P = 2a + 2b, dove 'a' e 'b' sono le lunghezze dei due lati diversi.
Rombo: Se il quadrilatero è un rombo (tutti i lati uguali, ma angoli diversi da 90 gradi), il perimetro è P = 4a, dove 'a' è la lunghezza di un lato.
Parallelogramma: Se il quadrilatero è un parallelogramma (lati opposti uguali e paralleli), il perimetro è P = 2a + 2b, dove 'a' e 'b' sono le lunghezze dei due lati diversi.
Trapezio: Se il quadrilatero è un trapezio, è necessario conoscere la lunghezza di ciascun lato per poter calcolare il perimetro.

Prisma con Base Pentagonale, Esagonale e Altri Poligoni

Il principio rimane lo stesso: sommare le lunghezze di tutti i lati del poligono. Per un pentagono, P = a + b + c + d + e. Per un esagono, P = a + b + c + d + e + f, e così via.

Poligoni Regolari: Se il poligono è regolare (tutti i lati e tutti gli angoli uguali), il perimetro è semplicemente P = n * a, dove 'n' è il numero di lati e 'a' è la lunghezza di un lato. Ad esempio, per un pentagono regolare, P = 5a; per un esagono regolare, P = 6a.

Cosa Fare Quando Non Conosci Tutte le Lunghezze dei Lati?

A volte, potresti non conoscere direttamente la lunghezza di tutti i lati del poligono di base. In questi casi, potresti aver bisogno di utilizzare altre informazioni, come:

Teorema di Pitagora: Se la base è un triangolo rettangolo e conosci la lunghezza di due lati, puoi usare il teorema di Pitagora (a² + b² = c²) per trovare la lunghezza del terzo lato.
Trigonometria: Se conosci la lunghezza di un lato e la misura di uno o più angoli, puoi usare le funzioni trigonometriche (seno, coseno, tangente) per trovare la lunghezza degli altri lati.
Proprietà Geometriche: Conoscere le proprietà specifiche del poligono di base (ad esempio, che è un triangolo equilatero o un quadrato) può semplificare il calcolo del perimetro.
Informazioni Supplementari: Il problema potrebbe fornirti altre informazioni, come l'area del poligono di base, che possono essere utilizzate per dedurre la lunghezza dei lati.

Esempio: Supponiamo di avere un prisma con base rettangolare. Conosciamo la lunghezza di un lato (a = 5 cm) e l'area del rettangolo (A = 20 cm²). Possiamo calcolare la lunghezza dell'altro lato usando la formula dell'area del rettangolo (A = a * b). Quindi, b = A / a = 20 cm² / 5 cm = 4 cm. Infine, possiamo calcolare il perimetro: P = 2a + 2b = 2 * 5 cm + 2 * 4 cm = 18 cm.

Errori Comuni da Evitare

Ecco alcuni errori comuni che è bene evitare quando si calcola il perimetro di base di un prisma:

Confondere il perimetro con l'area: Il perimetro è la lunghezza del contorno, mentre l'area è la misura della superficie.
Utilizzare unità di misura diverse: Assicurati che tutte le lunghezze siano espresse nella stessa unità di misura prima di sommarle.
Dimenticare di sommare tutti i lati: Verifica di aver considerato tutti i lati del poligono di base.
Applicare formule errate: Usa la formula corretta in base alla forma del poligono di base.
Non considerare le proprietà specifiche del poligono: Sfrutta le proprietà del poligono (ad esempio, se è regolare) per semplificare il calcolo.

Un Punto di Vista Diverso: Considerazioni Finali

Alcuni potrebbero obiettare che, nell'era della tecnologia, calcolare manualmente il perimetro di base di un prisma sia un'attività superflua, dato che esistono numerosi strumenti online e app che possono farlo automaticamente. È vero, la tecnologia può essere di grande aiuto, ma comprendere i principi fondamentali della geometria e saper eseguire i calcoli manualmente offre diversi vantaggi:

Maggiore Comprensione: Calcolare manualmente il perimetro ti aiuta a comprendere meglio il concetto di perimetro e le proprietà dei poligoni.
Problem Solving: Ti permette di sviluppare le tue capacità di problem solving e di ragionamento logico.
Verifica dei Risultati: Ti consente di verificare l'accuratezza dei risultati ottenuti con gli strumenti tecnologici.
Applicazioni Pratiche: Ti fornisce le competenze necessarie per affrontare problemi pratici che richiedono il calcolo del perimetro, anche in situazioni in cui non hai accesso a strumenti tecnologici.

Quindi, anche se la tecnologia è uno strumento prezioso, non sottovalutare l'importanza di acquisire una solida comprensione dei concetti fondamentali e di saper eseguire i calcoli manualmente. La vera padronanza di un argomento risiede nella comprensione profonda dei suoi principi, non solo nella capacità di utilizzare uno strumento per ottenere un risultato.

Spero che questo articolo ti sia stato utile e ti abbia fornito una guida chiara e semplice per calcolare il perimetro di base di un prisma. Ora, prova a mettere in pratica ciò che hai imparato risolvendo alcuni esercizi. Ricorda, la pratica rende perfetti!

Quale tipo di prisma ti incuriosisce di più e vorresti esplorare ulteriormente le sue proprietà geometriche?