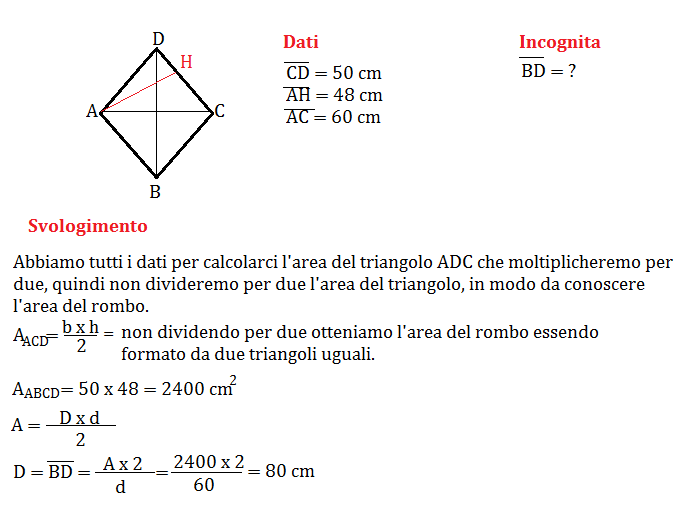
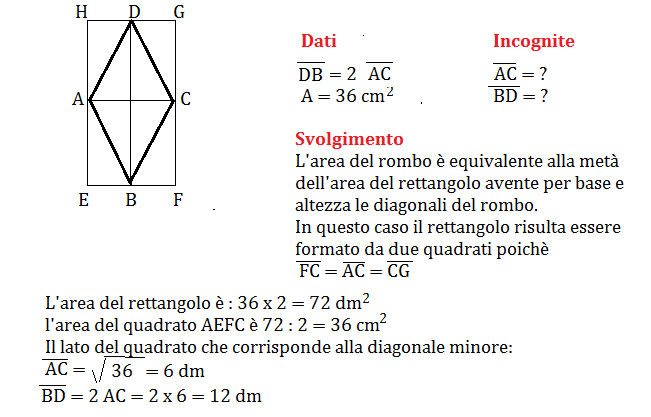
Come Si Calcola Il Perimetro Del Rombo Con Le Diagonali

Ciao a tutti! Oggi vorrei parlare di un concetto di geometria che, a prima vista, potrebbe sembrare semplicemente una formula, ma che in realtà nasconde una miriade di opportunità per affinare il nostro pensiero critico e la nostra capacità di risolvere problemi: il perimetro del rombo.
Spesso, quando ci troviamo di fronte a un problema matematico, l'approccio più comune è cercare subito la formula risolutiva. Questo è comprensibile, perché vogliamo ottenere la risposta in modo rapido ed efficiente. Ma vi invito a fare un passo indietro, a rallentare un po' e a considerare la bellezza che si cela dietro i numeri e le forme.
Esplorando il Rombo: Simmetria e Armonia
Il rombo, con la sua eleganza e la sua perfetta simmetria, è una figura geometrica che merita la nostra attenzione. Tutti e quattro i suoi lati sono uguali, il che lo rende una figura particolarmente armoniosa. Ma cosa succede quando non conosciamo la lunghezza del lato e ci vengono fornite le diagonali? È qui che la magia della matematica entra in gioco!
Il Teorema di Pitagora: Un Amico Fidato
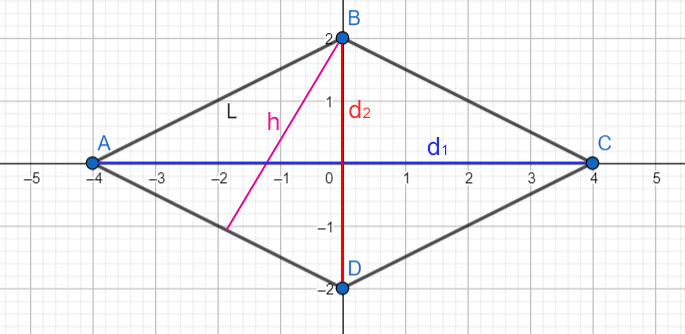
Per calcolare il perimetro di un rombo conoscendo le diagonali, dobbiamo fare ricorso a un vecchio amico: il teorema di Pitagora. Questo teorema, che lega i lati di un triangolo rettangolo, è uno strumento incredibilmente potente e versatile. Immaginate il rombo come quattro triangoli rettangoli identici, ognuno formato da metà di una diagonale e da un lato del rombo (l'ipotenusa).
Se chiamiamo le diagonali *d1* e *d2*, allora metà delle diagonali saranno *d1/2* e *d2/2*. Ora, per trovare la lunghezza del lato del rombo (che è l'ipotenusa del triangolo rettangolo), possiamo usare il teorema di Pitagora:
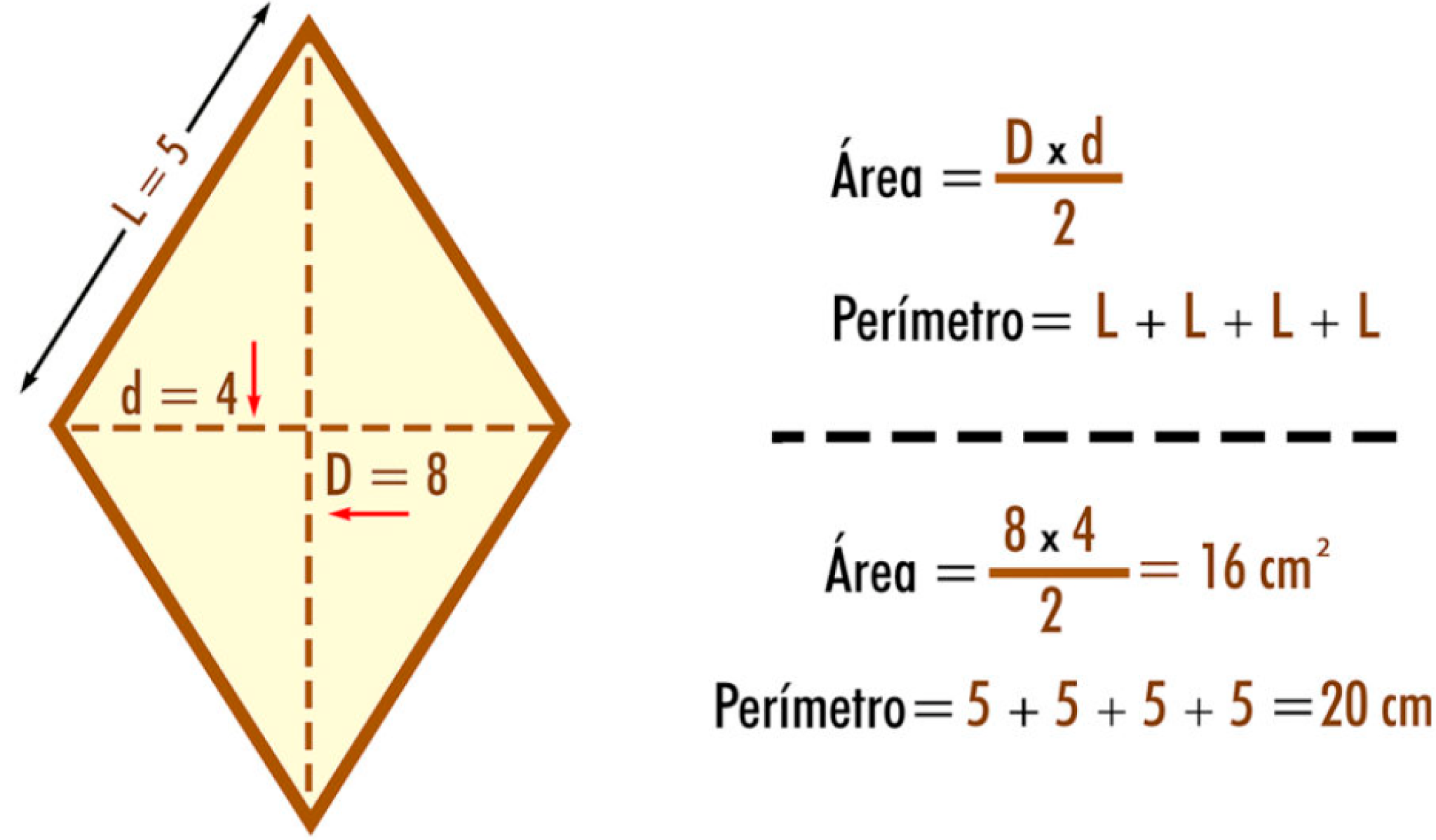
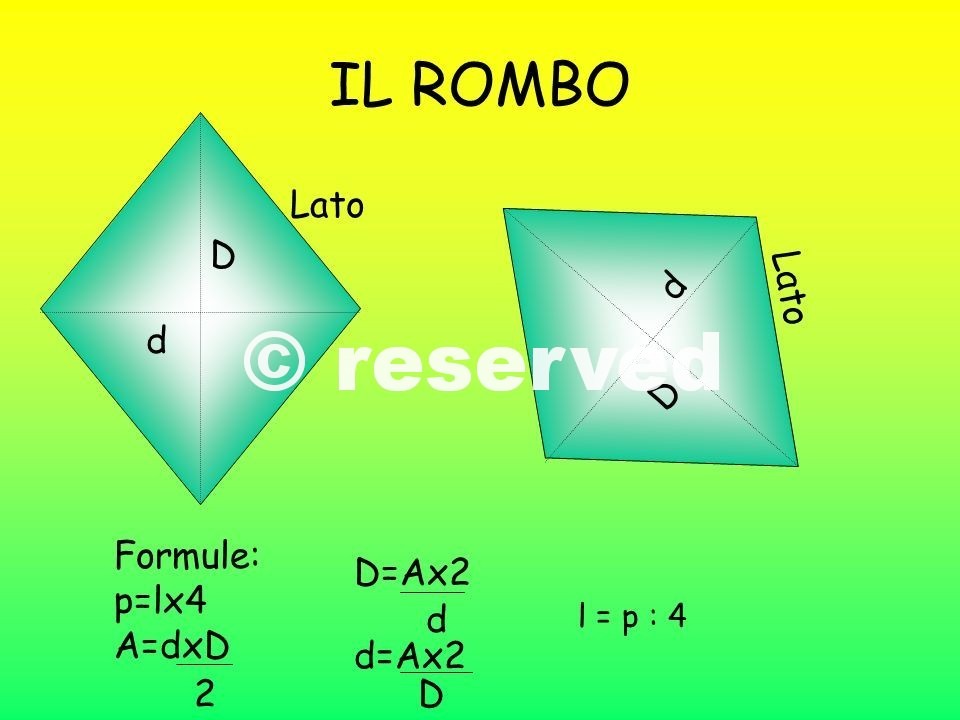
lato = √( (d1/2)² + (d2/2)² )
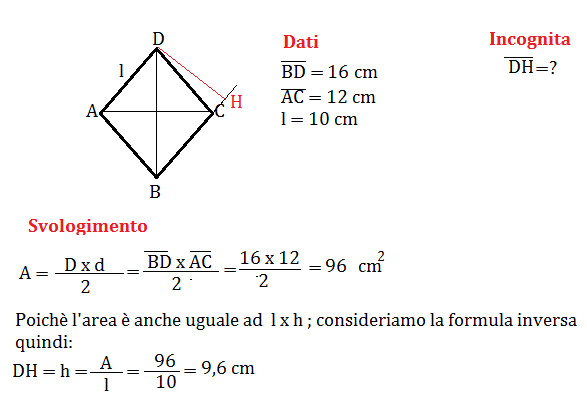
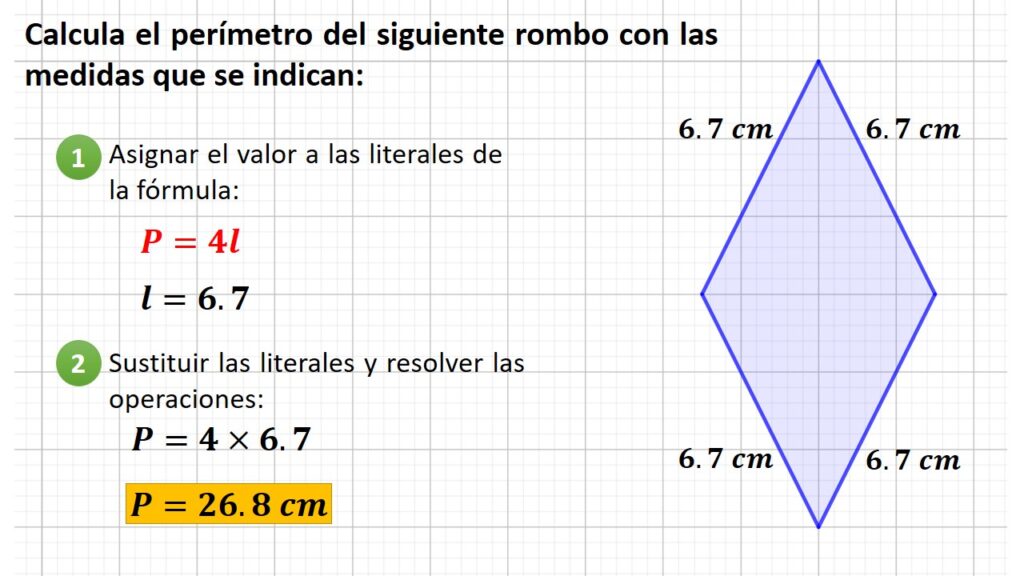
Una volta che abbiamo trovato la lunghezza del lato, il calcolo del perimetro diventa semplice: basta moltiplicare la lunghezza del lato per 4, dato che tutti i lati del rombo sono uguali.
Oltre la Formula: Un Viaggio nella Scoperta
Ma l'importanza di questo esercizio non si limita al semplice calcolo numerico. Ci insegna a scomporre un problema complesso in parti più piccole e gestibili. Ci insegna a individuare le relazioni tra le diverse grandezze coinvolte. Ci insegna, soprattutto, a fidarci delle nostre capacità di ragionamento e a non aver paura di affrontare le sfide.
Ricordate, la matematica non è solo un insieme di regole e formule da memorizzare. È un linguaggio, un modo di pensare, un'avventura intellettuale che ci permette di esplorare il mondo che ci circonda con occhi nuovi. Ogni problema risolto è una piccola vittoria, una conferma della nostra capacità di apprendere e crescere.
Quando vi trovate di fronte a un problema di geometria, o a qualsiasi altra sfida, non abbiate fretta di trovare la soluzione. Prendetevi del tempo per capire il problema, per esplorare le diverse possibilità, per sperimentare e imparare dai vostri errori. L'importante non è arrivare subito alla risposta giusta, ma godersi il viaggio della scoperta. E ricordate: l'umiltà di ammettere di non sapere e la perseveranza di non arrendersi sono qualità fondamentali per qualsiasi studente, e per qualsiasi persona.
Spero che questa riflessione vi sia stata utile e che vi abbia ispirato a guardare la matematica con occhi diversi. Buon studio a tutti!
Non dimenticate, la curiosità è la scintilla che accende la passione per l'apprendimento!