Come Si Calcola Area Del Trapezio

Hai mai guardato un borsone, una borsa o magari una fetta di torta e pensato: "Questa forma mi ricorda qualcosa..."? Probabilmente stavi pensando a un trapezio! Questa figura geometrica, apparentemente semplice, si nasconde in molti oggetti di uso quotidiano. Ma come si calcola l'area di questa forma così versatile? Questa guida è pensata per te, studente di scuola media o superiore, appassionato di geometria, o semplicemente curioso di rinfrescare le tue conoscenze. Ti guideremo passo dopo passo, con esempi pratici e spiegazioni chiare, alla scoperta della formula e del suo utilizzo.

Cos'è un Trapezio?

Prima di tuffarci nei calcoli, cerchiamo di definire con precisione cosa intendiamo per trapezio. Si tratta di un quadrilatero (una figura geometrica con quattro lati) che ha la caratteristica di avere due lati paralleli, chiamati basi. Gli altri due lati, invece, non sono paralleli e sono chiamati lati obliqui.

Esistono diverse tipologie di trapezi:

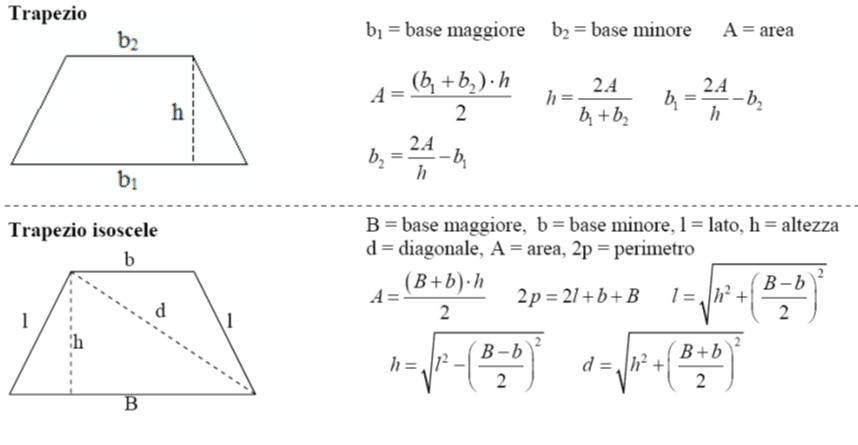
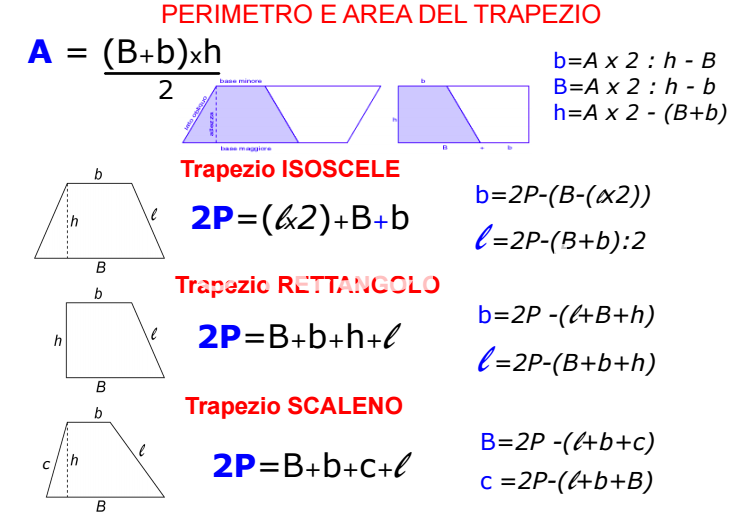
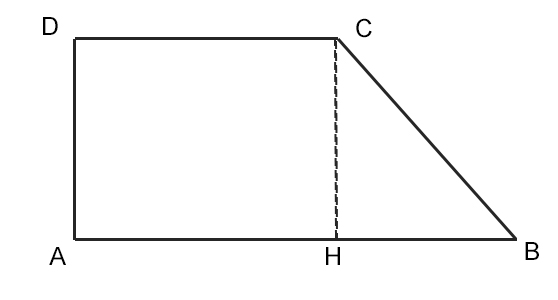
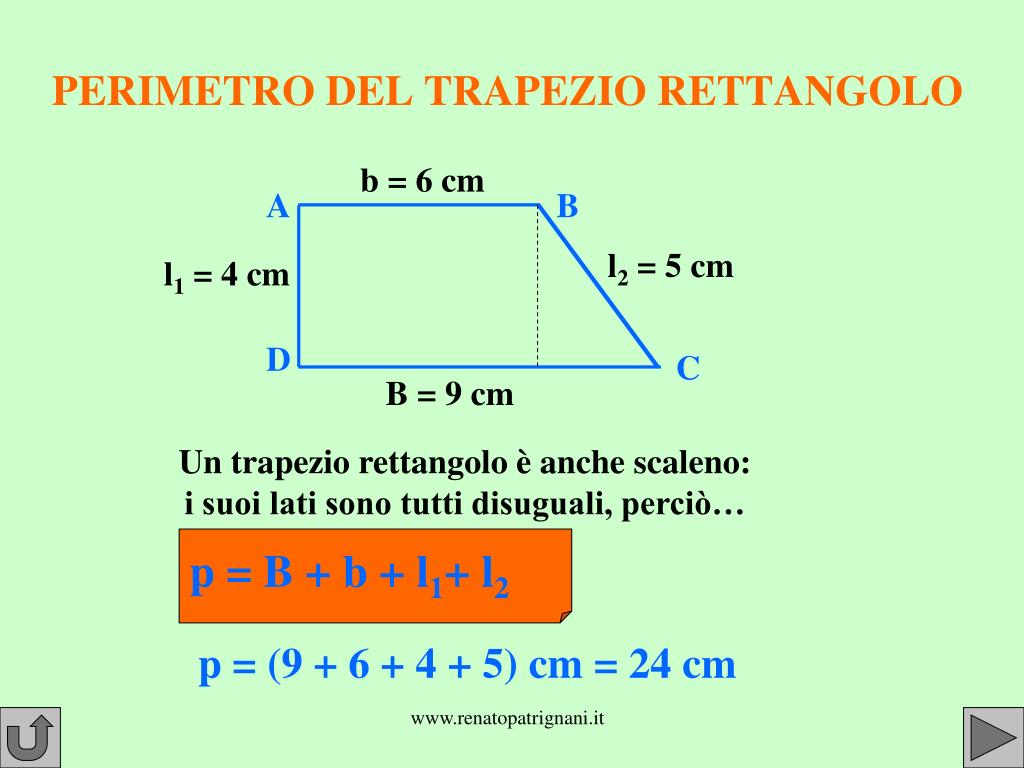
Trapezio Rettangolo: Ha due angoli retti (angoli di 90 gradi). Un lato obliquo è perpendicolare alle basi.
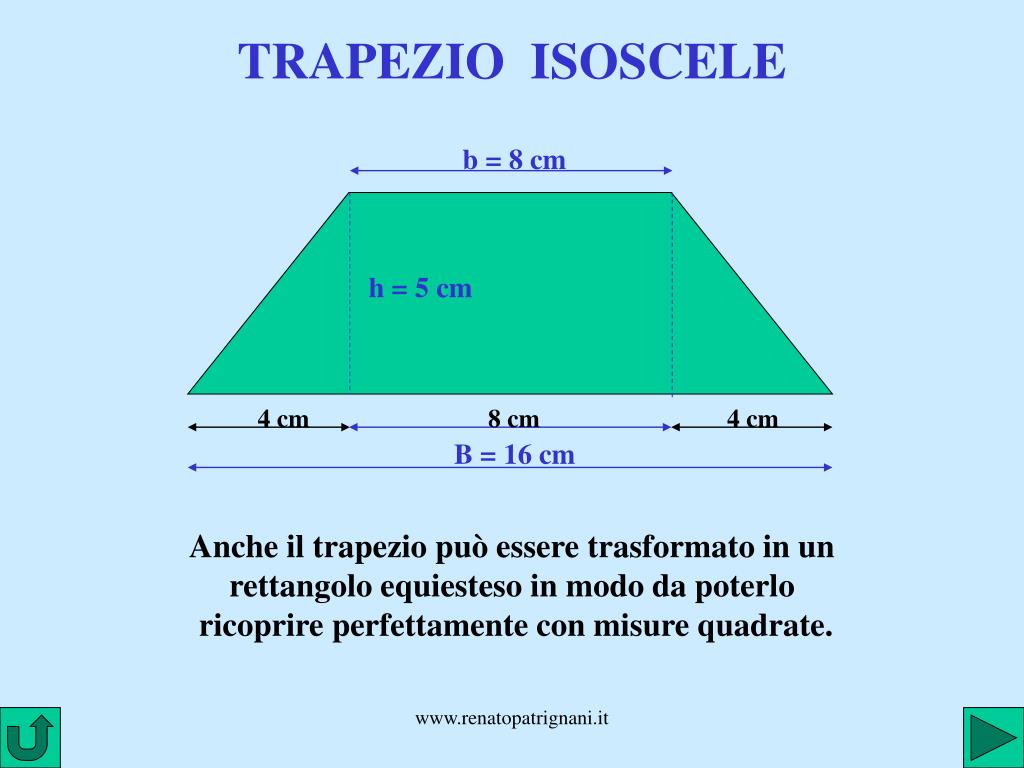
Trapezio Isoscele: I lati obliqui sono congruenti (hanno la stessa lunghezza). Anche gli angoli adiacenti a ciascuna base sono congruenti.
Trapezio Scaleno: Tutti i lati e tutti gli angoli sono diversi tra loro.

Non importa di che tipo di trapezio si tratti, la formula per calcolare l'area rimane la stessa! E questa è un'ottima notizia!

La Formula Magica: Come Calcolare l'Area del Trapezio

Eccoci al cuore del nostro articolo: la formula per calcolare l'area del trapezio. Preparati, è più semplice di quanto pensi!

L'area del trapezio si calcola utilizzando la seguente formula:

Area = (Base Maggiore + Base Minore) * Altezza / 2

Cerchiamo di capire cosa significano tutti questi termini:

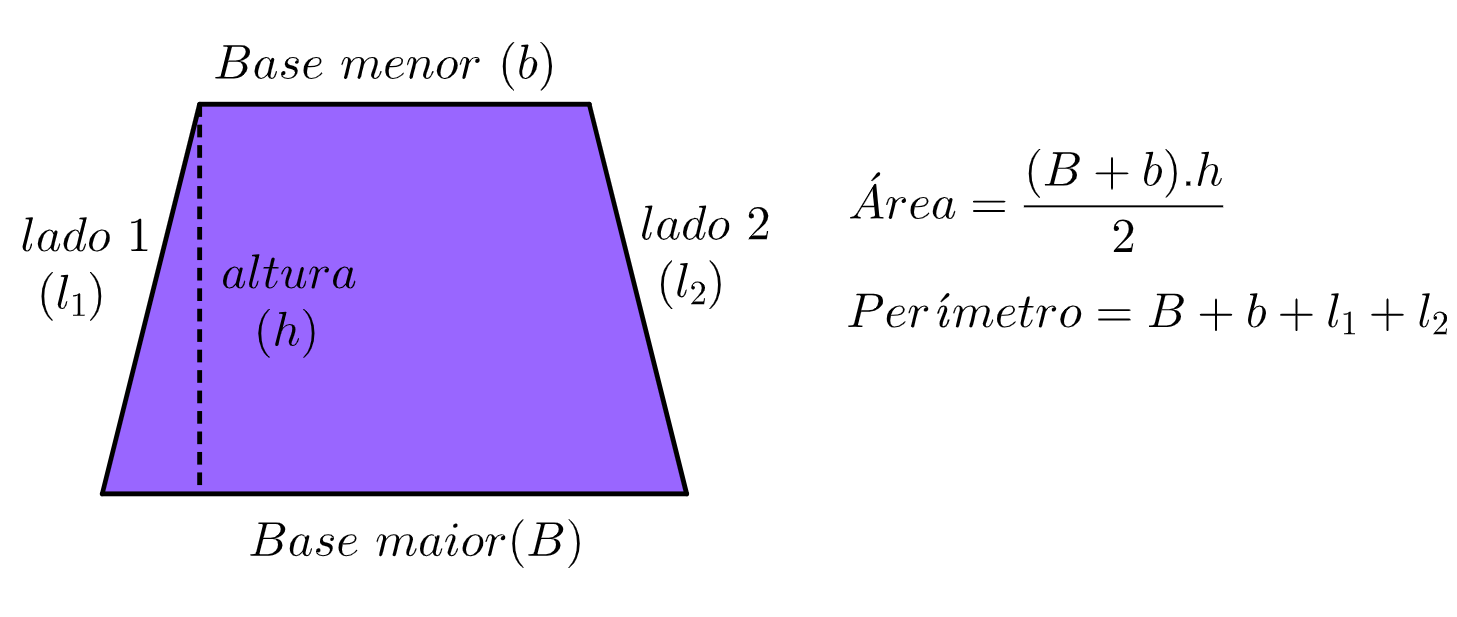
Base Maggiore (B): È il lato parallelo più lungo del trapezio.
Base Minore (b): È il lato parallelo più corto del trapezio.
Altezza (h): È la distanza perpendicolare tra le due basi. Immagina di tracciare una linea retta che collega le due basi, formando un angolo di 90 gradi con entrambe. La lunghezza di questa linea è l'altezza.

In sostanza, sommiamo le lunghezze delle due basi, moltiplichiamo il risultato per l'altezza e dividiamo tutto per due. Fatto! Abbiamo l'area del trapezio!

Esempio Pratico: Mettiamo alla Prova la Formula

Per rendere tutto più chiaro, vediamo un esempio pratico. Immagina di avere un trapezio con le seguenti misure:

Base Maggiore (B) = 10 cm
Base Minore (b) = 6 cm
Altezza (h) = 4 cm

Applichiamo la formula:

Area = (10 cm + 6 cm) * 4 cm / 2

Area = (16 cm) * 4 cm / 2

Area = 64 cm² / 2

Area = 32 cm²

Quindi, l'area del trapezio è di 32 centimetri quadrati.

Un Altro Esempio per Consolidare

Proviamo con un altro esempio, questa volta con misure diverse:

Base Maggiore (B) = 15 metri
Base Minore (b) = 8 metri
Altezza (h) = 6 metri

Applichiamo nuovamente la formula:

Area = (15 m + 8 m) * 6 m / 2

Area = (23 m) * 6 m / 2

Area = 138 m² / 2

Area = 69 m²

In questo caso, l'area del trapezio è di 69 metri quadrati.

Perché Funziona Questa Formula? Una Spiegazione Intuitiva

Magari ti stai chiedendo: "Ma perché questa formula funziona? Da dove salta fuori?" Cerchiamo di capire la logica che c'è dietro.

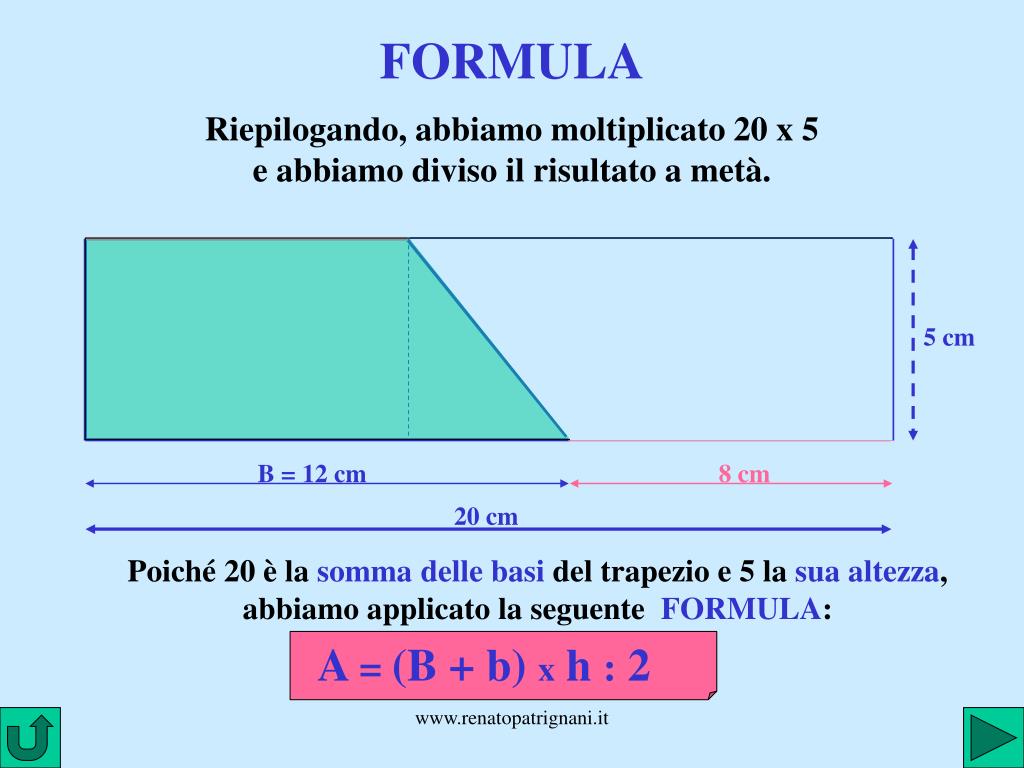
Possiamo immaginare di "tagliare" il trapezio e trasformarlo in un rettangolo equivalente. Per fare questo, immaginiamo di prendere un triangolo dal lato obliquo sinistro del trapezio e di "incollarlo" al lato obliquo destro, in modo da formare un rettangolo.

La base di questo rettangolo sarà la media aritmetica delle due basi del trapezio: (Base Maggiore + Base Minore) / 2. L'altezza del rettangolo sarà la stessa altezza del trapezio.

Quindi, l'area del rettangolo (e quindi l'area del trapezio) sarà: (Base Maggiore + Base Minore) / 2 * Altezza, che è esattamente la formula che abbiamo imparato!

Trucchi e Consigli Utili

Ecco alcuni suggerimenti che ti torneranno utili quando dovrai calcolare l'area di un trapezio:

Identifica correttamente le basi: Ricorda che le basi sono i due lati paralleli del trapezio. Non confonderli con i lati obliqui.
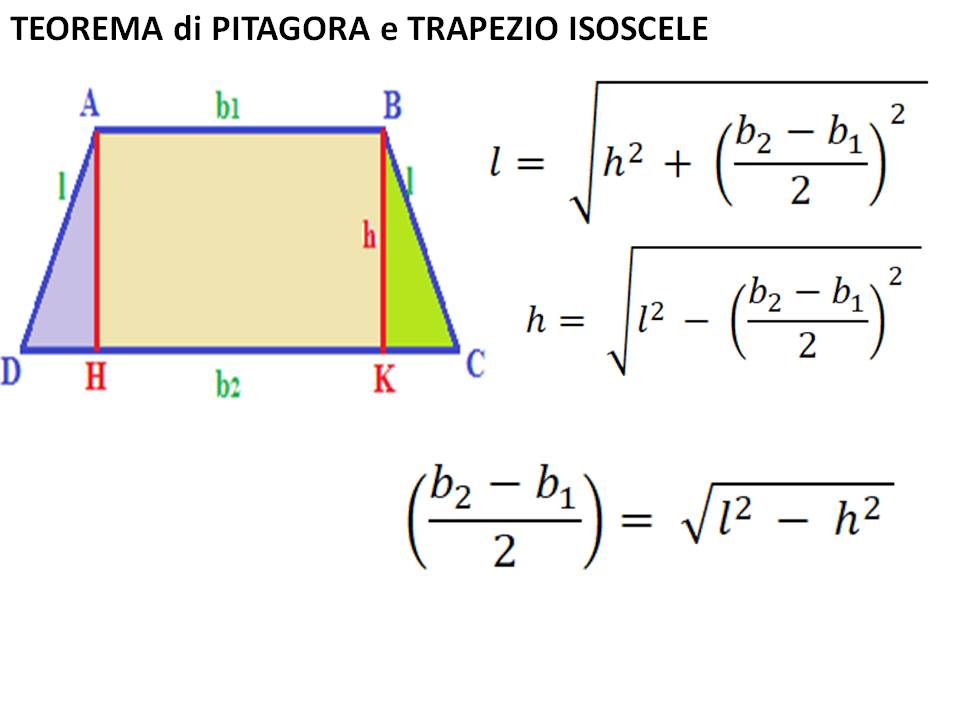
L'altezza è fondamentale: Assicurati di utilizzare la distanza perpendicolare tra le basi. Se ti viene fornita la lunghezza di un lato obliquo, non usarla come altezza! Potrebbe essere necessario calcolare l'altezza utilizzando il teorema di Pitagora, se hai sufficienti informazioni.
Unità di misura: Assicurati che tutte le misure siano nella stessa unità di misura (ad esempio, tutti in centimetri o tutti in metri). Se hai misure in unità diverse, convertile prima di applicare la formula.
Controlla i risultati: Dopo aver calcolato l'area, ricontrolla i tuoi calcoli per evitare errori.
Disegna il trapezio: Disegnare il trapezio può aiutarti a visualizzare il problema e a identificare le basi e l'altezza.

Esercizi di Pratica

Per padroneggiare veramente il calcolo dell'area del trapezio, è fondamentale fare pratica. Ecco alcuni esercizi che puoi provare a risolvere:

Un trapezio ha una base maggiore di 12 cm, una base minore di 8 cm e un'altezza di 5 cm. Calcola la sua area.
Un trapezio rettangolo ha una base maggiore di 18 metri, una base minore di 10 metri e il lato obliquo perpendicolare alle basi lungo 7 metri. Calcola la sua area.
Un trapezio isoscele ha una base maggiore di 20 cm, una base minore di 14 cm e i lati obliqui lunghi 5 cm. Calcola la sua area (suggerimento: dovrai usare il teorema di Pitagora per trovare l'altezza).

Dove Troviamo i Trapezi nella Vita Reale?

Come abbiamo detto all'inizio, i trapezi sono più comuni di quanto pensiamo! Ecco alcuni esempi:

Borse e borsoni: Molte borse e borsoni hanno una forma trapezoidale.
Fette di torta: Quando tagli una torta a spicchi, ogni fetta ha una forma approssimativamente trapezoidale.
Tetti di case: Alcuni tetti hanno una forma trapezoidale.
Segnali stradali: Alcuni segnali stradali, come il segnale di "Dare precedenza", hanno una forma trapezoidale.
Finestre: Alcune finestre hanno una forma trapezoidale, specialmente nelle architetture più moderne.

Conclusione: L'Area del Trapezio a Portata di Mano

Congratulazioni! Ora sai come calcolare l'area del trapezio. Ricorda la formula: Area = (Base Maggiore + Base Minore) * Altezza / 2. Fai pratica con gli esercizi, cerca i trapezi che ti circondano nella vita di tutti i giorni e presto sarai un vero esperto di geometria!

Speriamo che questa guida ti sia stata utile e che tu abbia trovato le risposte che cercavi. La matematica, quando spiegata in modo chiaro e semplice, può essere davvero affascinante! Non smettere mai di imparare e di esplorare il meraviglioso mondo della geometria!