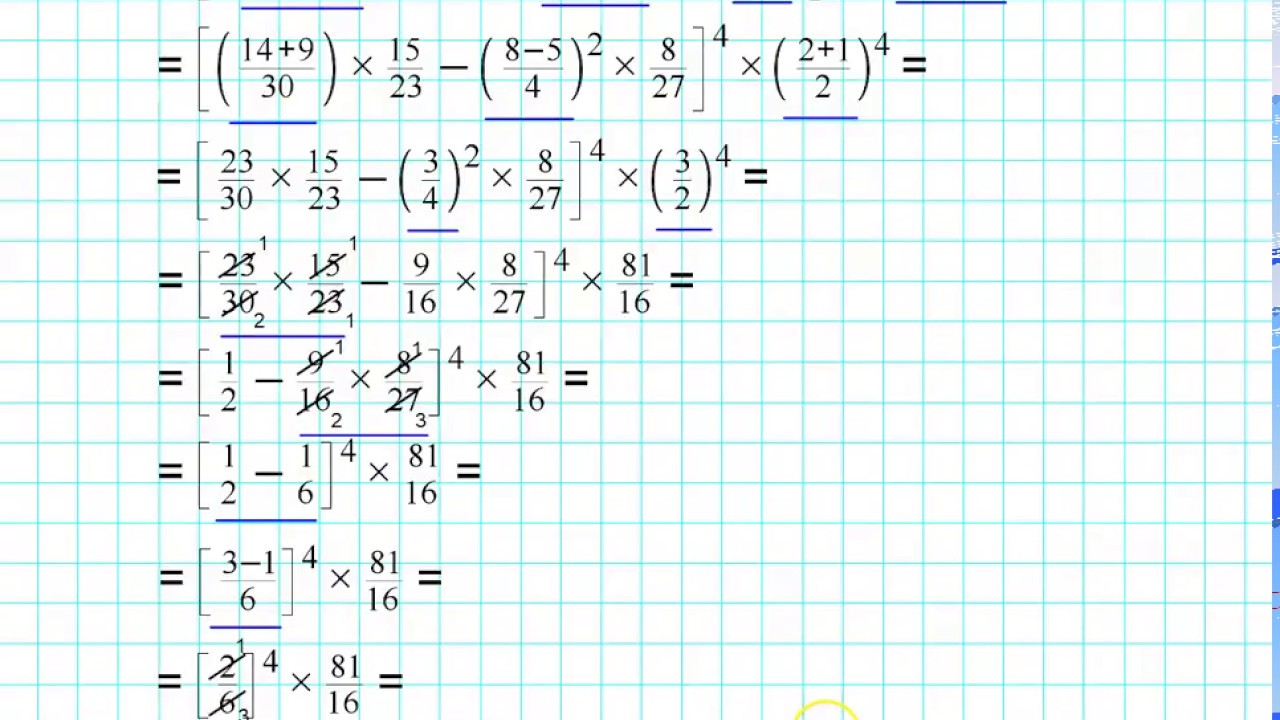
Come Risolvere Espressioni Con Le Frazioni

Ciao a tutti! Immaginate per un attimo le frazioni non come ostacoli matematici, ma come piccoli tasselli di un mosaico affascinante. Certo, all'inizio possono sembrare un po' disordinati, un po' enigmatici, ma con un pizzico di pazienza e tanta curiosità, scoprirete che nascondono segreti e bellezza.
Affrontare le espressioni con le frazioni è un'occasione per affinare il nostro spirito di osservazione. Ogni frazione, ogni operazione, è una pista da seguire, un indizio per arrivare alla soluzione. Iniziamo con calma, come esploratori in un territorio sconosciuto.
Il Segreto è l'Ordine
Il primo passo è abbracciare l'ordine. Ricordiamoci la gerarchia delle operazioni: prima le parentesi, poi le moltiplicazioni e divisioni, infine addizioni e sottrazioni. Questa regola, come una bussola, ci guida attraverso il labirinto delle frazioni.
Denominatori Comuni: Amici che semplificano la vita
Le frazioni, spesso, non amano stare da sole con denominatori diversi. Trovare il denominatore comune è come farle incontrare, farle dialogare. Pensate al minimo comune multiplo (mcm) come a un linguaggio universale che permette loro di comunicare efficacemente. Trasformare le frazioni in modo che abbiano lo stesso denominatore rende le operazioni molto più semplici e lineari. È un po' come tradurre un testo in una lingua che tutti comprendono!
Dalla Teoria alla Pratica: Un Passo alla Volta
Dopo aver uniformato i denominatori, le addizioni e le sottrazioni diventano quasi un gioco. Si sommano o si sottraggono i numeratori, mantenendo il denominatore comune. Ricordatevi, ogni passo deve essere eseguito con attenzione, come se steste dipingendo un quadro. Un piccolo errore può rovinare l'intera opera, ma non temete, si può sempre ricominciare!
Moltiplicazione e Divisione: Danze Armoniose
La moltiplicazione delle frazioni è un ballo elegante: si moltiplicano i numeratori tra loro e i denominatori tra loro. Nessun bisogno di denominatori comuni qui! La divisione, invece, è un po' più audace. Dividere per una frazione è come moltiplicare per il suo inverso. Capovolgiamo la seconda frazione e via, la divisione si trasforma in moltiplicazione! Ricordatevi che la matematica, come la vita, è piena di trasformazioni inaspettate.
Non scoraggiamoci di fronte alle difficoltà. Gli errori sono opportunità di apprendimento. Ogni volta che sbagliamo, abbiamo la possibilità di capire dove abbiamo commesso l'errore e come evitarlo in futuro. L'importante è non perdere mai la curiosità e la voglia di imparare.
A volte, potremmo sentirci sopraffatti dalla complessità delle espressioni con le frazioni. In questi momenti, respiriamo profondamente e ricordiamoci che non siamo soli. Chiedere aiuto è un segno di forza, non di debolezza. Confrontiamoci con i nostri compagni, chiediamo spiegazioni al nostro insegnante. L'apprendimento è un viaggio condiviso.
E infine, non dimentichiamo mai l'importanza della perseveranza. La matematica, come qualsiasi altra disciplina, richiede impegno e dedizione. Non scoraggiamoci se non riusciamo a risolvere un'espressione al primo tentativo. Continuiamo a provare, a sperimentare, a esplorare. Alla fine, la soddisfazione di aver superato una difficoltà è impagabile.
Imparare a risolvere espressioni con le frazioni non è solo un esercizio matematico. È un allenamento per la nostra mente, un'opportunità per sviluppare il nostro pensiero critico e la nostra capacità di risolvere problemi. È un invito a crescere con umiltà, riconoscendo i nostri limiti e sforzandoci di superarli. Allora, pronti a tuffarvi nel mondo affascinante delle frazioni?