Come Fare I Problemi Di Geometria

Affrontare i problemi di geometria può sembrare un'impresa ardua per molti. Ti senti frustrato quando ti siedi alla scrivania, con un libro pieno di figure e formule che sembrano incomprensibili? Non sei solo. Molti studenti, e anche adulti, lottano con la geometria. La buona notizia è che con le strategie giuste e un po' di pazienza, la geometria può diventare accessibile e persino piacevole.

Immagina di essere un architetto che progetta un edificio, un ingegnere che costruisce un ponte, o persino un artista che crea un'opera d'arte. Tutti questi professionisti utilizzano i principi della geometria per dare forma alle loro idee. La geometria non è solo un esercizio accademico, ma uno strumento potente che ci permette di comprendere e modellare il mondo che ci circonda. Capire la geometria significa quindi capire una parte fondamentale della realtà.

Alcuni potrebbero pensare che la geometria sia troppo astratta e lontana dalla vita reale, che sia un insieme di regole e formule senza un vero significato. Altri potrebbero credere di non essere "portati" per la matematica, e quindi la geometria sia un ostacolo insormontabile. Ma queste sono solo convinzioni limitanti. Con l'approccio giusto, chiunque può imparare e padroneggiare la geometria.

Capire il Problema: La Chiave per la Soluzione

Il primo passo per risolvere un problema di geometria è capire a fondo di cosa si tratta. Non limitarti a leggere il testo una sola volta. Analizza attentamente ogni parola, ogni numero e ogni figura.

Leggi attentamente il testo: Identifica le informazioni importanti e quello che il problema ti chiede di trovare.
Disegna una figura: La geometria è una materia visiva. Un disegno accurato ti aiuterà a visualizzare il problema e a individuare le relazioni tra gli elementi.
Etichetta la figura: Assegna nomi ai punti, alle linee, agli angoli e alle figure. Questo ti permetterà di comunicare in modo chiaro e preciso.
Scrivi le informazioni date: Elenca tutte le informazioni che il problema ti fornisce, come le lunghezze dei lati, le misure degli angoli, o le relazioni tra le figure.
Identifica cosa devi trovare: Definisci chiaramente cosa ti viene richiesto di calcolare o dimostrare.

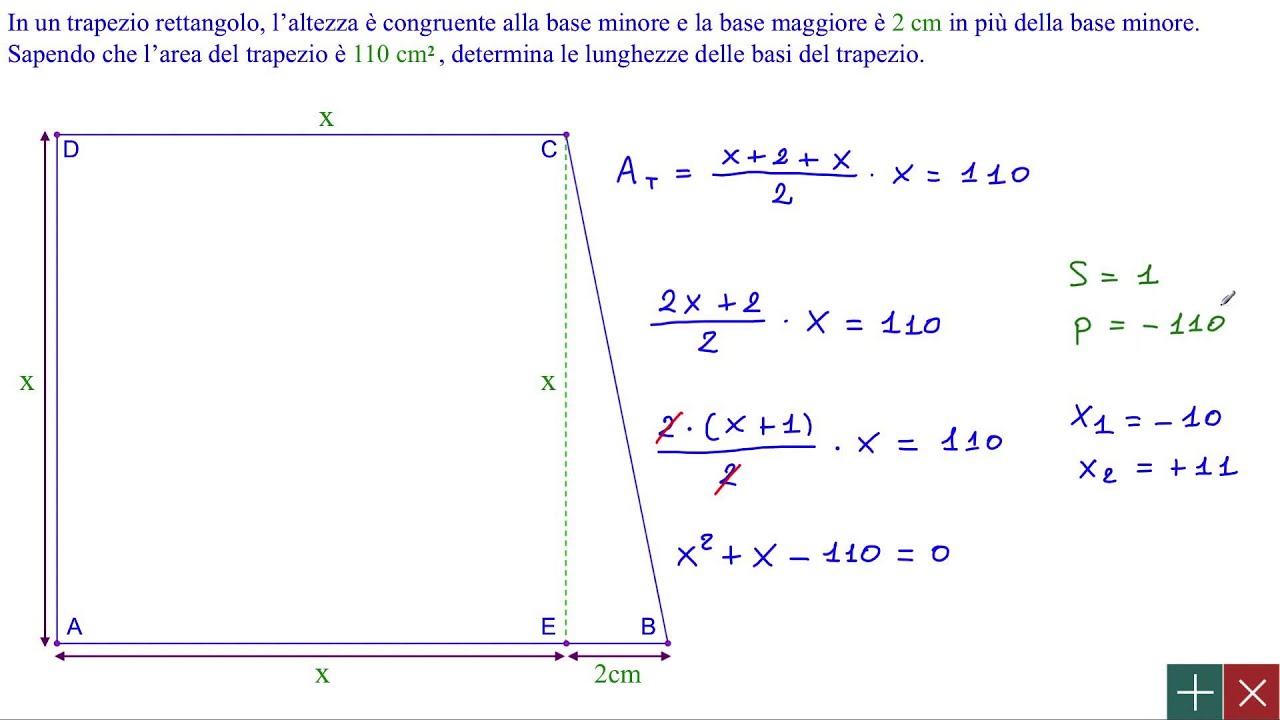
Un esempio pratico: Immagina un problema che ti chiede di calcolare l'area di un triangolo isoscele con base di 10 cm e altezza di 8 cm. Dopo aver letto il problema, disegna un triangolo isoscele, etichetta la base con "10 cm" e l'altezza con "8 cm". Ora sai esattamente cosa devi fare: calcolare l'area di questo triangolo.

Conoscere le Formule e i Teoremi Fondamentali

La geometria si basa su un insieme di formule e teoremi fondamentali. Conoscerli è essenziale per risolvere i problemi. Non si tratta solo di memorizzarli, ma di capirne il significato e di saperli applicare correttamente.

Formule Essenziali:

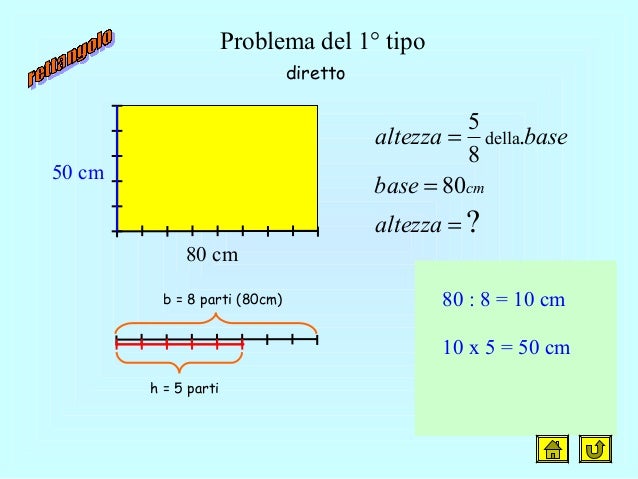
Area del triangolo: (base x altezza) / 2
Area del quadrato: lato x lato
Area del rettangolo: base x altezza
Area del cerchio: π x raggio²
Perimetro del triangolo: somma dei lati
Perimetro del quadrato: 4 x lato
Perimetro del rettangolo: 2 x (base + altezza)
Circonferenza del cerchio: 2 x π x raggio

Teoremi Chiave:

Teorema di Pitagora: In un triangolo rettangolo, il quadrato dell'ipotenusa è uguale alla somma dei quadrati dei cateti (a² + b² = c²).
Teorema di Talete: Se due rette parallele sono tagliate da una trasversale, gli angoli corrispondenti sono congruenti.
Criteri di congruenza dei triangoli: SAS (lato-angolo-lato), ASA (angolo-lato-angolo), SSS (lato-lato-lato).
Criteri di similitudine dei triangoli: AA (angolo-angolo), SAS (lato-angolo-lato), SSS (lato-lato-lato).

Ricorda, non devi imparare tutto a memoria in una sola volta. Inizia con le formule e i teoremi più semplici, e poi aggiungi gradualmente quelli più complessi. L'importante è capire come e quando applicarli.

Scomporre il Problema in Sotto-Problemi

Spesso, i problemi di geometria possono sembrare complessi e intimidatori. Un modo efficace per affrontarli è scomporli in problemi più piccoli e gestibili. Questo approccio ti permette di concentrarti su un aspetto del problema alla volta, rendendo il processo di risoluzione più semplice e meno stressante.

Identifica le figure geometriche: Riconosci le figure geometriche presenti nel problema (triangoli, quadrati, cerchi, ecc.).
Trova le relazioni tra le figure: Analizza come le figure sono collegate tra loro (intersecano, sono tangenti, sono parallele, ecc.).
Applica le formule e i teoremi: Utilizza le formule e i teoremi appropriati per calcolare le grandezze che ti servono.
Verifica i risultati: Controlla che i risultati ottenuti siano coerenti con le informazioni date e con le proprietà delle figure geometriche.

Ad esempio, se devi calcolare l'area di una figura complessa, potresti dividerla in figure più semplici, come triangoli e rettangoli. Calcola l'area di ciascuna figura separatamente, e poi somma i risultati per ottenere l'area totale.

Esercitarsi, Esercitarsi, Esercitarsi!

Come in ogni disciplina, la pratica è fondamentale per padroneggiare la geometria. Risolvi molti problemi, di diversa difficoltà, per acquisire familiarità con le formule, i teoremi e le strategie di risoluzione. Più ti eserciti, più diventerai bravo a riconoscere i modelli, a individuare le soluzioni e a evitare gli errori.

Inizia con problemi semplici: Non cercare di risolvere subito i problemi più difficili. Inizia con esercizi più semplici per consolidare le tue conoscenze di base.
Aumenta gradualmente la difficoltà: Man mano che acquisisci sicurezza, prova a risolvere problemi più complessi.
Utilizza diverse risorse: Sfrutta i libri di testo, gli eserciziari, i siti web e i video tutorial per trovare problemi e soluzioni.
Chiedi aiuto: Non aver paura di chiedere aiuto al tuo insegnante, ai tuoi compagni di classe o a un tutor se hai difficoltà.
Analizza i tuoi errori: Quando sbagli un problema, cerca di capire perché hai sbagliato e cosa puoi fare per evitarlo in futuro.

Ricorda che l'errore è una parte naturale del processo di apprendimento. Non scoraggiarti se non riesci a risolvere un problema subito. Analizza i tuoi errori, impara da essi e continua a esercitarti.

L'Importanza della Visualizzazione

La geometria è una disciplina intrinsecamente visiva. Sviluppare la tua capacità di visualizzare le figure geometriche nello spazio ti aiuterà enormemente a risolvere i problemi. Cerca di immaginare le figure ruotate, riflesse, o trasformate in diversi modi. Questo ti permetterà di individuare le relazioni tra gli elementi e di trovare le soluzioni più facilmente.

Utilizza software di geometria dinamica: Strumenti come GeoGebra ti permettono di disegnare e manipolare figure geometriche in modo interattivo, aiutandoti a visualizzare i concetti.
Costruisci modelli: Costruire modelli fisici delle figure geometriche può essere utile per comprendere le loro proprietà e le loro relazioni.
Immagina le figure in movimento: Cerca di immaginare le figure ruotate, riflesse, o traslate nello spazio.
Utilizza colori diversi: Colorare le diverse parti di una figura può aiutarti a distinguerle e a individuare le relazioni tra loro.

Sviluppare la tua capacità di visualizzazione ti darà un vantaggio significativo nella risoluzione dei problemi di geometria. La geometria è un linguaggio visivo, e imparare a "parlarlo" ti aprirà nuove prospettive.

Ricorda la Logica

La geometria non riguarda solo formule e calcoli, ma anche logica e ragionamento. Molti problemi richiedono di dimostrare una proprietà o di dedurre una conclusione a partire da un insieme di ipotesi. Sviluppare le tue capacità di ragionamento logico ti aiuterà a risolvere questi tipi di problemi.

Impara le regole della logica: Familiarizzati con i principi del ragionamento deduttivo e induttivo.
Costruisci argomentazioni valide: Impara a formulare argomentazioni chiare e coerenti per dimostrare le tue affermazioni.
Identifica le fallacie logiche: Impara a riconoscere gli errori di ragionamento che possono portare a conclusioni errate.
Utilizza diagrammi di Venn: I diagrammi di Venn possono essere utili per visualizzare le relazioni tra insiemi e per risolvere problemi di logica.

La geometria è un'arte del ragionamento. Imparare a pensare in modo logico e critico ti aiuterà non solo a risolvere i problemi di geometria, ma anche a prendere decisioni migliori nella tua vita di tutti i giorni.

Superare la paura e l'avversione per la geometria è possibile. Richiede impegno, pratica e un approccio strategico. Ricorda di concentrarti sulla comprensione dei concetti, sulla visualizzazione delle figure e sull'applicazione delle formule e dei teoremi. Non aver paura di chiedere aiuto e di imparare dai tuoi errori.

Con la giusta mentalità e le giuste strategie, la geometria può diventare un'esperienza gratificante e stimolante. E chissà, potresti persino scoprire di avere un talento nascosto per la matematica!

Ora, rifletti: qual è il primo passo che intraprenderai oggi per affrontare un problema di geometria che ti sta bloccando?