Come Calcolare L'apotema Di Una Piramide A Base Quadrata
Capita a tutti di sentirsi un po' smarriti di fronte alla geometria, soprattutto quando si parla di figure solide come le piramidi. Calcolare l'apotema di una piramide a base quadrata può sembrare complicato all'inizio, ma non disperare! Con un po' di pazienza e la giusta guida, anche tu potrai padroneggiare questo concetto. In questo articolo, ti accompagnerò passo dopo passo, rendendo il processo chiaro, semplice e, spero, persino divertente!
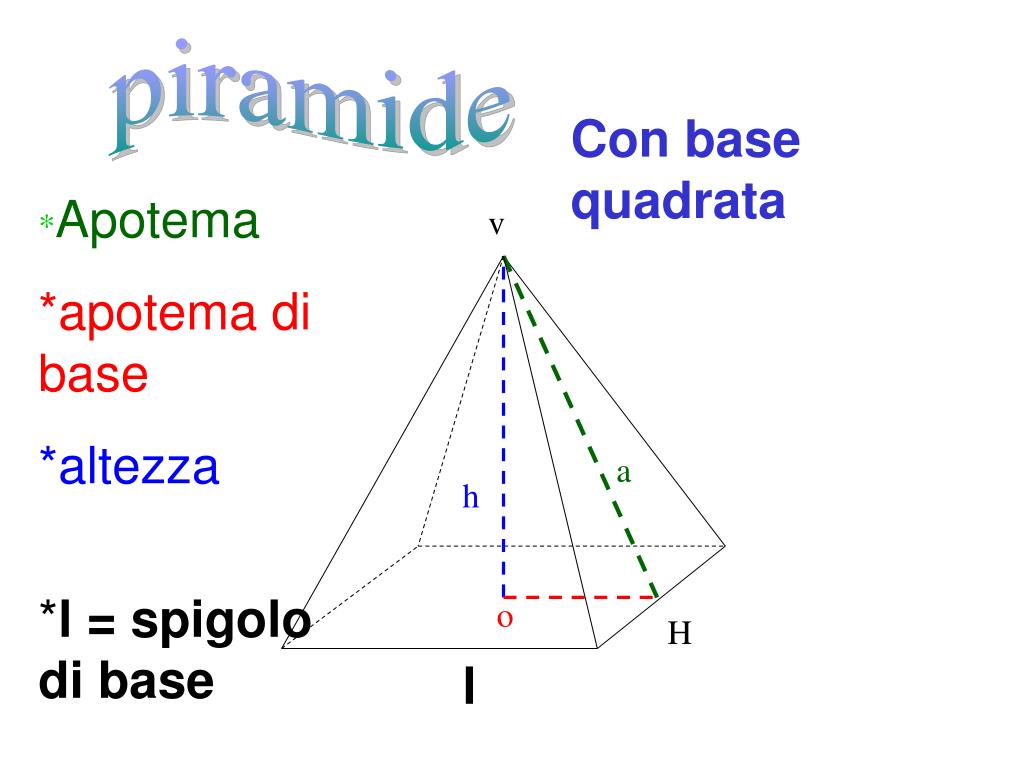
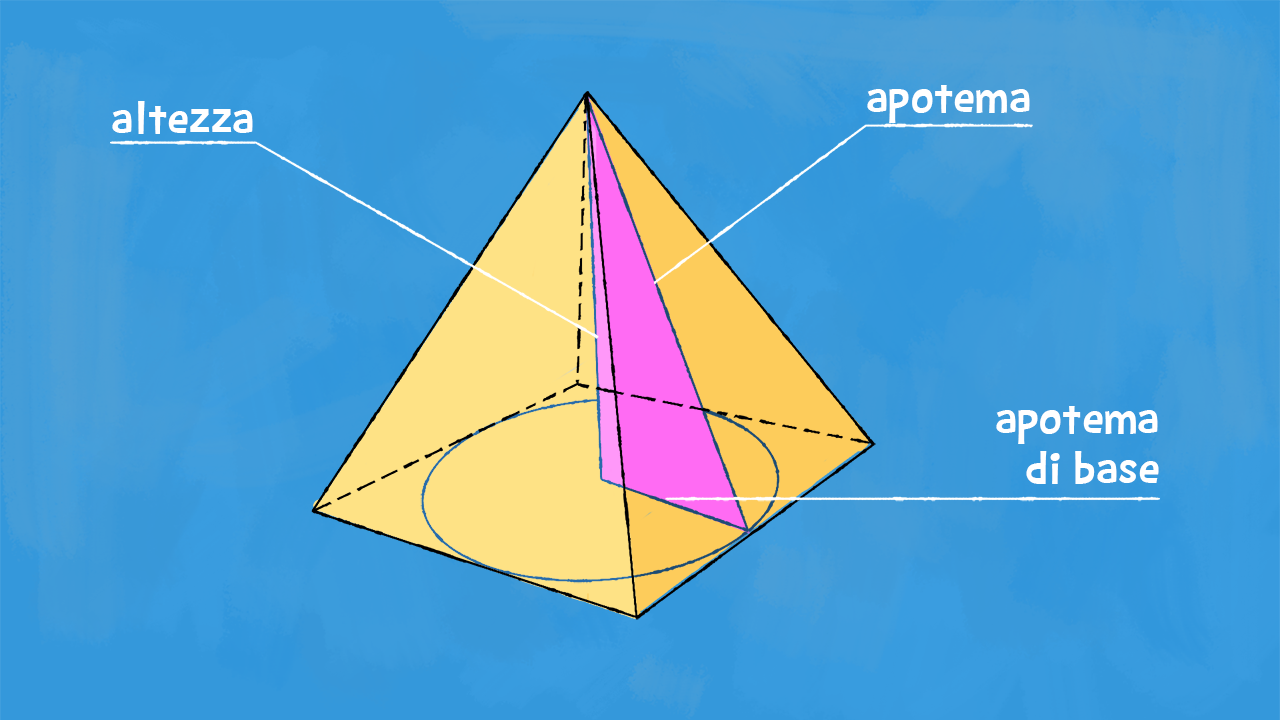
Cos'è l'Apotema di una Piramide a Base Quadrata?
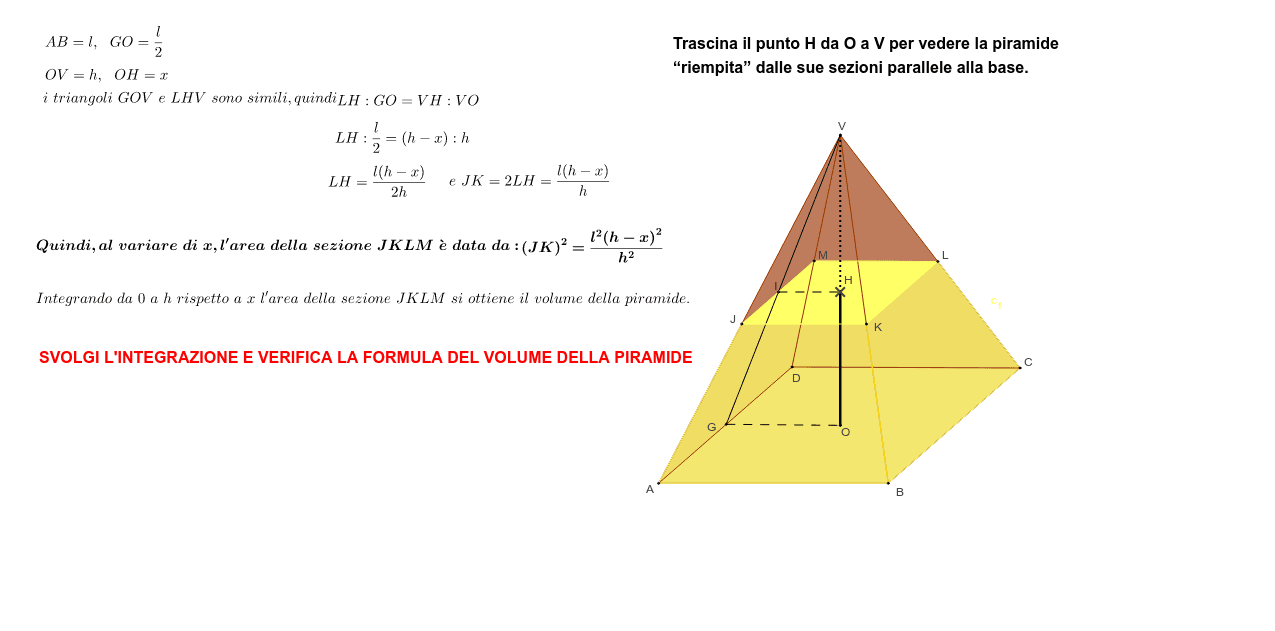
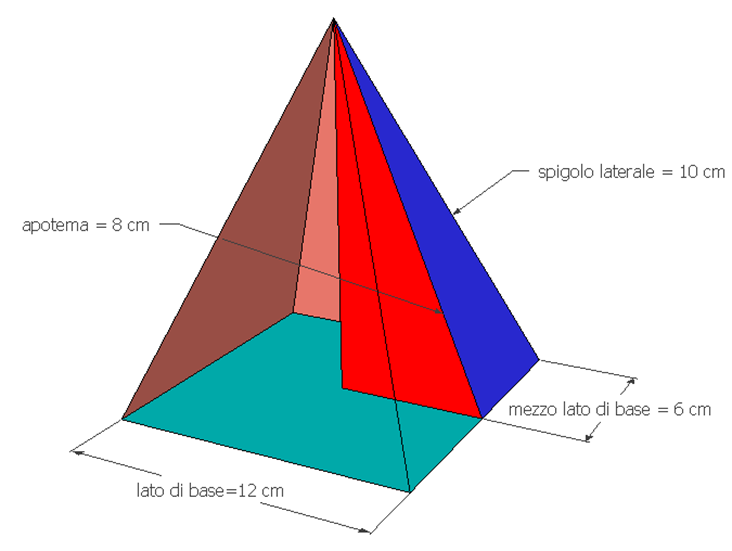
Prima di iniziare con i calcoli, è fondamentale capire di cosa stiamo parlando. L'apotema di una piramide a base quadrata non è l'altezza della piramide. Immagina una delle facce triangolari che compongono la piramide. L'apotema è l'altezza di questo triangolo, misurata dal vertice della piramide fino al punto medio del lato della base quadrata.
Visualizzarlo è cruciale. Pensa a una fetta di pizza tagliata dal centro di una pizza quadrata. L'apotema è la distanza dal punto della fetta al centro del bordo.
Perché è Importante Sapere Calcolarlo?
Calcolare l'apotema non è solo un esercizio teorico. Conoscere l'apotema ti permette di:
* Calcolare l'area laterale della piramide: L'area laterale è la somma delle aree di tutte le facce triangolari. * Calcolare l'area totale della piramide: Sommando l'area laterale all'area della base. * Risolvere problemi di geometria solida: Molti problemi di geometria richiedono la conoscenza dell'apotema per trovare volumi o altre dimensioni. * Applicazioni pratiche: Dalla progettazione architettonica alla modellazione 3D, la comprensione delle figure solide è fondamentale.Metodo 1: Usando il Teorema di Pitagora
Questo è il metodo più comune e, a mio parere, il più intuitivo. Si basa sul famosissimo teorema di Pitagora: a² + b² = c²
Per applicarlo, dobbiamo visualizzare un triangolo rettangolo all'interno della piramide:
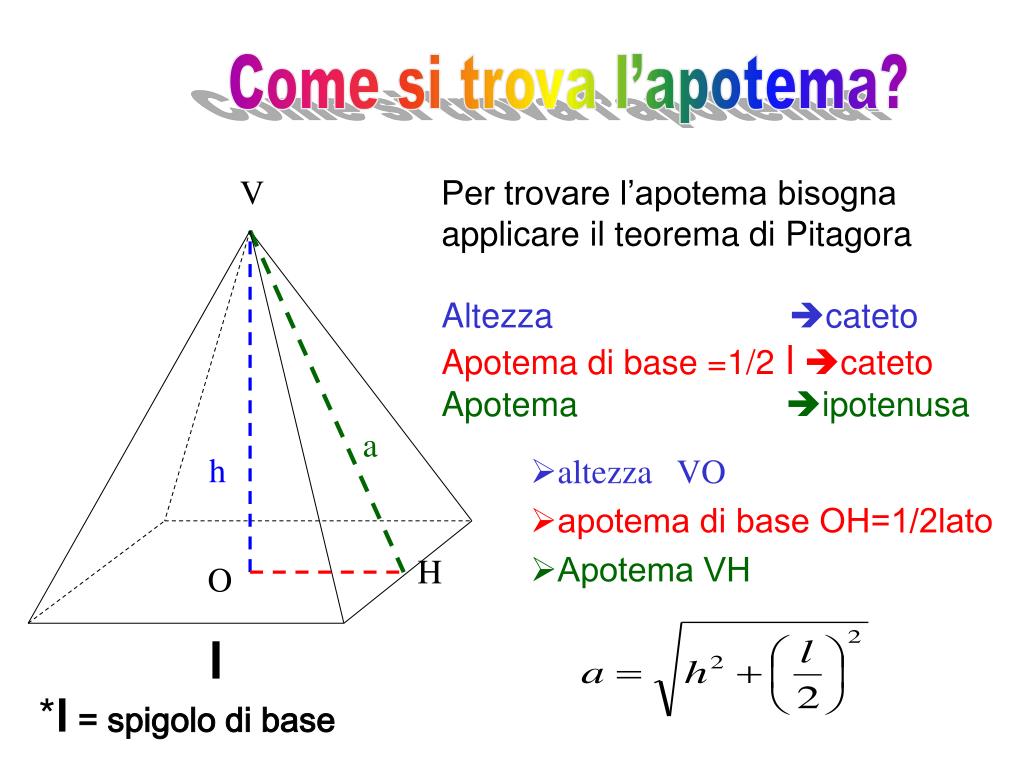
* L'altezza della piramide (h): È un cateto del triangolo rettangolo. * Metà della lunghezza del lato della base (l/2): È l'altro cateto del triangolo rettangolo. * L'apotema (a): È l'ipotenusa del triangolo rettangolo.Quindi, possiamo scrivere la formula:
a² = h² + (l/2)²Per trovare l'apotema (a), dobbiamo estrarre la radice quadrata di entrambi i lati dell'equazione:
a = √(h² + (l/2)²)Esempio Pratico
Supponiamo di avere una piramide a base quadrata con un'altezza (h) di 4 cm e un lato della base (l) di 6 cm. Calcoliamo l'apotema:
1. Calcola metà del lato della base: l/2 = 6 cm / 2 = 3 cm 2. Eleva al quadrato l'altezza e metà del lato della base: h² = 4² = 16 cm² e (l/2)² = 3² = 9 cm² 3. Somma i risultati: 16 cm² + 9 cm² = 25 cm² 4. Estrai la radice quadrata: √25 cm² = 5 cmQuindi, l'apotema della piramide è di 5 cm.
Consigli Utili
* Disegna sempre un diagramma: Visualizzare la piramide e il triangolo rettangolo ti aiuterà a capire meglio la formula. * Presta attenzione alle unità di misura: Assicurati che tutte le misure siano espresse nella stessa unità (es. cm, metri, ecc.). * Usa una calcolatrice: Per semplificare i calcoli, soprattutto se i numeri sono decimali. * Verifica il tuo risultato: L'apotema deve essere maggiore dell'altezza della piramide e maggiore di metà del lato della base.Metodo 2: Conoscendo l'Area Laterale e il Lato della Base
Se conosci l'area laterale della piramide e la lunghezza del lato della base, puoi calcolare l'apotema in modo diverso. L'area laterale (Al) di una piramide a base quadrata è data dalla formula:
Al = 2 * l * aDove:
* Al = Area laterale * l = Lunghezza del lato della base * a = ApotemaPer trovare l'apotema, dobbiamo semplicemente riorganizzare la formula:
a = Al / (2 * l)Esempio Pratico
Supponiamo di avere una piramide a base quadrata con un'area laterale (Al) di 48 cm² e un lato della base (l) di 6 cm. Calcoliamo l'apotema:
1. Moltiplica il lato della base per 2: 2 * 6 cm = 12 cm 2. Dividi l'area laterale per il risultato: 48 cm² / 12 cm = 4 cmQuindi, l'apotema della piramide è di 4 cm.
Consigli Utili
* Assicurati di avere l'area laterale: Non confondere l'area laterale con l'area totale. * Rivedi la formula: Assicurati di aver riorganizzato correttamente la formula per trovare l'apotema. * Verifica il tuo risultato: Controlla che l'apotema abbia un valore ragionevole rispetto alle altre dimensioni della piramide.Metodo 3: Quando Hai l'Angolo al Vertice
Questo metodo è meno comune ma utile se conosci l'angolo al vertice di una delle facce triangolari. Chiameremo questo angolo θ (theta).
In questo caso, possiamo usare la trigonometria. Ricorda che l'apotema è l'ipotenusa di un triangolo rettangolo che ha come cateto opposto metà del lato della base (l/2). Possiamo usare la funzione seno:
sin(θ/2) = (l/2) / aRisolvendo per l'apotema (a):
a = (l/2) / sin(θ/2)Esempio Pratico
Supponiamo di avere una piramide a base quadrata con un lato della base (l) di 8 cm e un angolo al vertice (θ) di 60 gradi. Calcoliamo l'apotema:
1. Calcola metà del lato della base: l/2 = 8 cm / 2 = 4 cm 2. Calcola metà dell'angolo al vertice: θ/2 = 60 gradi / 2 = 30 gradi 3. Calcola il seno di 30 gradi: sin(30°) = 0.5 4. Dividi metà del lato della base per il seno: a = 4 cm / 0.5 = 8 cmQuindi, l'apotema della piramide è di 8 cm.
Consigli Utili
* Assicurati di usare i gradi: Le calcolatrici possono essere impostate in gradi o radianti. Verifica che la tua calcolatrice sia impostata sui gradi. * Usa una calcolatrice scientifica: Avrai bisogno di una calcolatrice scientifica per calcolare il seno dell'angolo. * Comprendi la trigonometria: Questo metodo richiede una conoscenza di base delle funzioni trigonometriche.L'Importanza della Pratica
Come per ogni abilità, la pratica rende perfetti. Non scoraggiarti se non capisci subito tutto. Prova a risolvere diversi problemi, partendo da quelli più semplici e aumentando gradualmente la difficoltà. Cerca esercizi online, nei libri di testo o chiedi aiuto al tuo insegnante.
Ricorda, la geometria è un linguaggio. Più lo parli, più diventerai fluente! Non avere paura di fare errori, perché sono un'opportunità per imparare e migliorare. Con la giusta dose di impegno e perseveranza, sarai in grado di calcolare l'apotema di una piramide a base quadrata con facilità e sicurezza.
Incoraggiare l'Apprendimento
Genitori e insegnanti possono svolgere un ruolo fondamentale nell'incoraggiare l'apprendimento della geometria:
* Rendete l'apprendimento divertente: Utilizzate giochi, puzzle e attività pratiche per rendere la geometria più coinvolgente. * Collegate la geometria al mondo reale: Mostrate come i concetti geometrici vengono utilizzati in architettura, arte, design e altre discipline. * Offrite supporto e incoraggiamento: Siate pazienti e comprensivi, e celebrate i progressi dei vostri figli o studenti. * Incoraggiate la curiosità: Ponete domande stimolanti e incoraggiate i bambini a esplorare e scoprire nuove cose.L'apprendimento della geometria non deve essere un compito arduo. Con il giusto approccio e un po' di creatività, può diventare un'esperienza stimolante e gratificante.