Come Calcolare L'ampiezza Di Un Angolo

Ti sei mai trovato di fronte a un angolo, chiedendoti: "Quanti gradi misura? Come faccio a capirlo?" Se la risposta è sì, non sei solo! Molti studenti, e non solo, si sentono spaesati di fronte alla geometria, in particolare quando si tratta di calcolare l'ampiezza di un angolo. Fortunatamente, esistono diversi metodi e strumenti per superare questa sfida. In questa guida, ti accompagnerò passo dopo passo, fornendoti le conoscenze e le tecniche necessarie per misurare gli angoli con sicurezza e precisione.

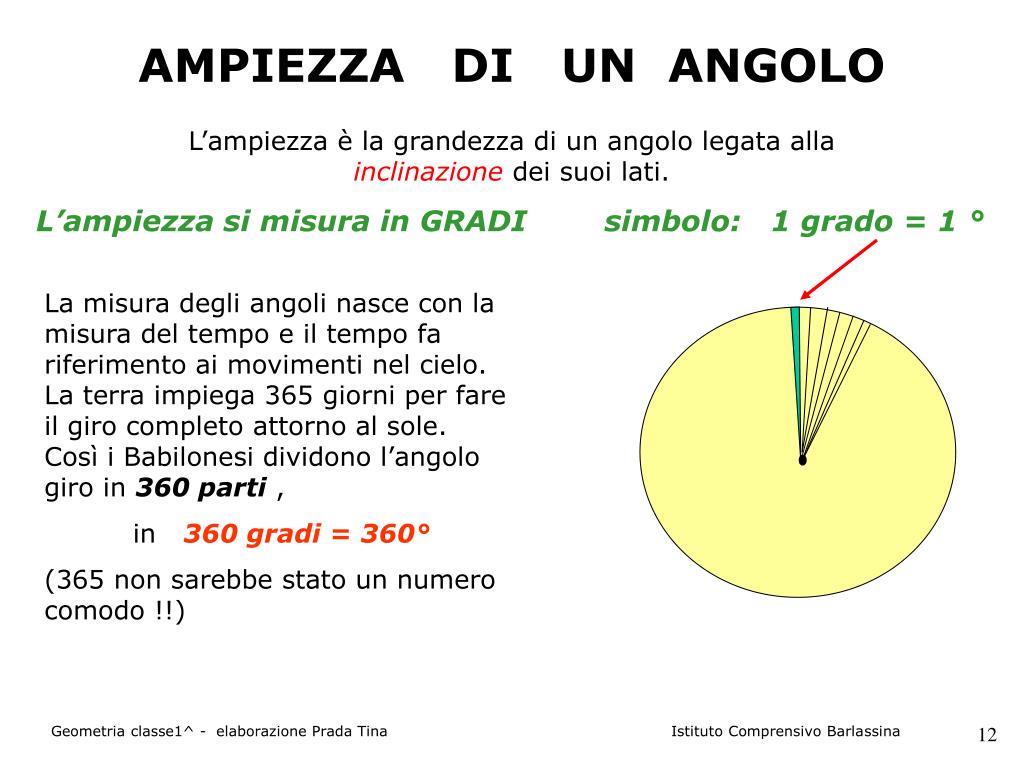
Capire le Basi: Cos'è un Angolo?

Prima di addentrarci nei calcoli, è fondamentale comprendere cos'è esattamente un angolo. In termini semplici, un angolo è la misura della rotazione tra due semirette che partono da uno stesso punto, chiamato vertice. Pensa alle lancette di un orologio: l'angolo che formano cambia continuamente man mano che il tempo scorre.

Gli angoli si misurano in gradi (°). Un cerchio completo corrisponde a 360°. Ecco alcune categorie di angoli comuni:

• Angolo acuto: Minore di 90°
• Angolo retto: Esattamente 90°
• Angolo ottuso: Maggiore di 90° e minore di 180°
• Angolo piatto: Esattamente 180°
• Angolo concavo: Maggiore di 180° e minore di 360°
• Angolo giro: Esattamente 360°

Conoscere queste definizioni è cruciale per poter identificare e misurare correttamente gli angoli.

Metodi per Calcolare l'Ampiezza di un Angolo

Esistono diversi modi per calcolare l'ampiezza di un angolo, a seconda delle informazioni che hai a disposizione. Esploriamo insieme i più comuni:

1. Utilizzo del Goniometro

Il goniometro è lo strumento più diretto e preciso per misurare gli angoli. Si tratta di un semicerchio o cerchio completo graduato, di solito in plastica trasparente. Ecco come usarlo:

1. Posiziona il centro del goniometro sul vertice dell'angolo.
2. Allinea lo 0° del goniometro a una delle semirette che formano l'angolo.
3. Leggi il valore in gradi dove l'altra semiretta interseca la scala del goniometro. Questo valore rappresenta l'ampiezza dell'angolo.

Consiglio pratico: Assicurati che il goniometro sia ben allineato per ottenere una misurazione accurata. Un piccolo errore di allineamento può portare a una misurazione sbagliata.

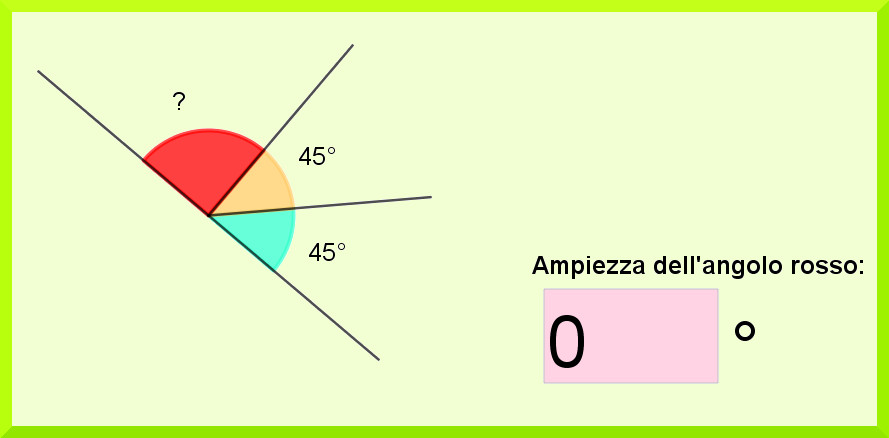
2. Calcoli con Angoli Complementari e Supplementari

A volte, non hai bisogno di un goniometro per trovare l'ampiezza di un angolo. Puoi sfruttare le relazioni tra angoli complementari e supplementari.

• Angoli complementari: Due angoli la cui somma è 90°. Se conosci l'ampiezza di uno dei due angoli complementari, puoi trovare l'altro sottraendo il valore conosciuto da 90°. Esempio: Se un angolo misura 30°, il suo complementare misura 90° - 30° = 60°.
• Angoli supplementari: Due angoli la cui somma è 180°. Similmente, se conosci l'ampiezza di uno dei due angoli supplementari, puoi trovare l'altro sottraendo il valore conosciuto da 180°. Esempio: Se un angolo misura 120°, il suo supplementare misura 180° - 120° = 60°.

Queste relazioni sono particolarmente utili in problemi di geometria che coinvolgono triangoli e altre figure.

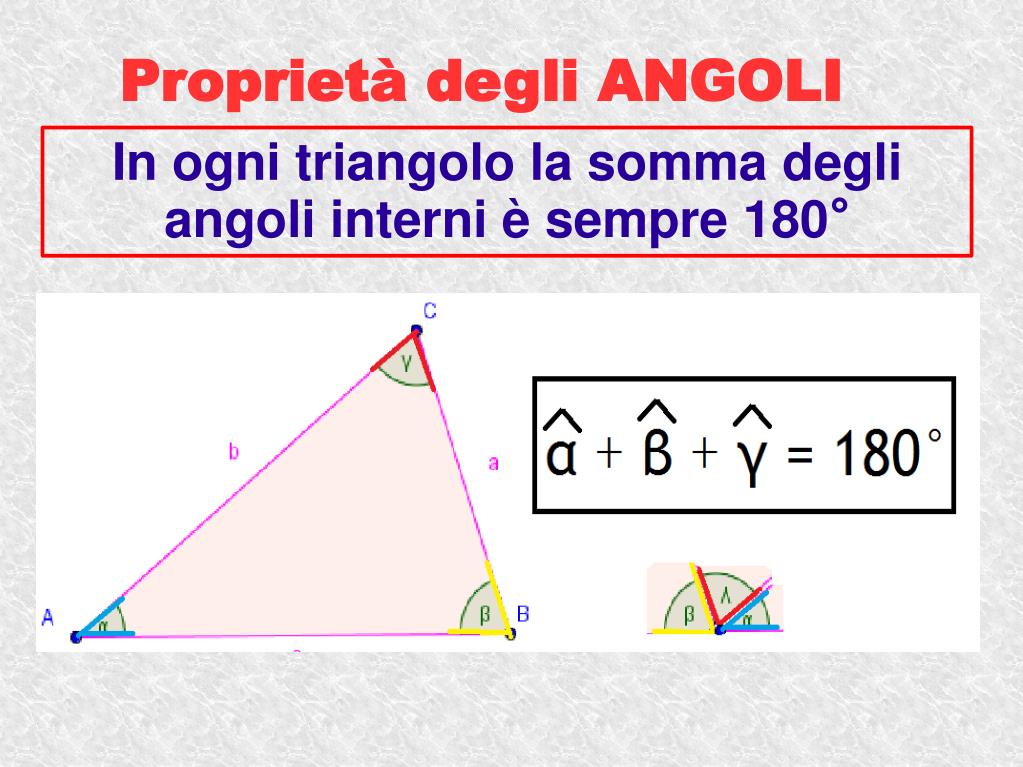
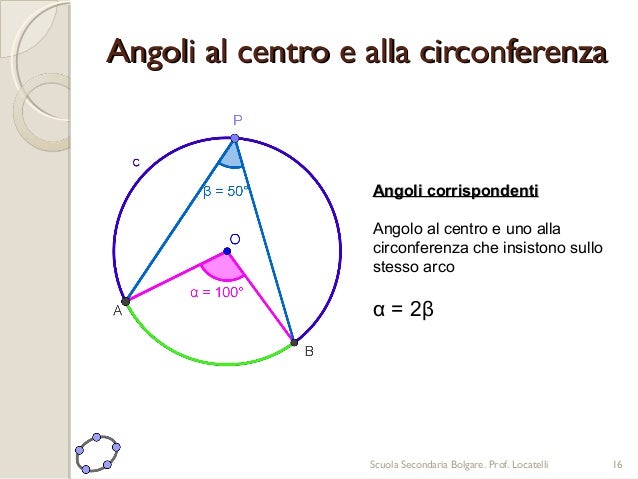
3. Relazioni Angolari in Triangoli

I triangoli offrono un contesto ricco per applicare concetti angolari. Ricorda che:

• La somma degli angoli interni di un triangolo è sempre 180°.
• In un triangolo rettangolo, un angolo misura 90°.
• In un triangolo isoscele, due angoli sono uguali.
• In un triangolo equilatero, tutti gli angoli misurano 60°.

Se conosci l'ampiezza di due angoli di un triangolo, puoi trovare il terzo semplicemente sottraendo la somma dei due angoli conosciuti da 180°. Questo è un principio fondamentale della geometria.

Esempio: In un triangolo, un angolo misura 45° e un altro 60°. Il terzo angolo misurerà 180° - (45° + 60°) = 180° - 105° = 75°.

4. Utilizzo di Rapporti Trigonometrici

Per gli angoli all'interno di triangoli rettangoli, puoi utilizzare i rapporti trigonometrici seno (sin), coseno (cos) e tangente (tan) per calcolare l'ampiezza dell'angolo, conoscendo la lunghezza dei lati.

Ricorda le definizioni:

• sin(angolo) = lato opposto / ipotenusa
• cos(angolo) = lato adiacente / ipotenusa
• tan(angolo) = lato opposto / lato adiacente

Una volta calcolato il valore del seno, coseno o tangente dell'angolo, puoi utilizzare le funzioni inverse (arcsin, arccos, arctan) sulla tua calcolatrice per trovare l'ampiezza dell'angolo in gradi. Assicurati che la calcolatrice sia impostata sulla modalità "gradi" (DEG) e non "radianti" (RAD).

Esempio: In un triangolo rettangolo, il lato opposto all'angolo che vuoi trovare misura 3 cm e l'ipotenusa misura 5 cm. Allora, sin(angolo) = 3/5 = 0.6. Utilizzando la funzione arcsin sulla calcolatrice, trovi che l'angolo misura circa 36.87°.

Strumenti e Risorse Utili

Oltre al goniometro fisico, esistono numerose risorse online che possono aiutarti a misurare gli angoli e a risolvere problemi di geometria:

• Calcolatrici online: Molte calcolatrici online offrono funzionalità trigonometriche e la possibilità di convertire tra diverse unità di misura angolare.
• Software di geometria dinamica: Programmi come GeoGebra permettono di costruire figure geometriche interattive e misurare angoli con precisione.
• App per smartphone: Esistono app che utilizzano la fotocamera del tuo telefono per misurare gli angoli in tempo reale.
• Tutorial e video online: Piattaforme come YouTube offrono una vasta gamma di tutorial che spiegano come calcolare gli angoli in diversi contesti.

Consigli Finali per il Successo

Calcolare l'ampiezza di un angolo può sembrare complicato all'inizio, ma con la pratica e la comprensione dei concetti base, diventerà un'abilità naturale. Ecco alcuni consigli finali:

• Pratica regolarmente: Risolvi diversi esercizi e problemi per rafforzare le tue capacità.
• Utilizza strumenti e risorse: Non aver paura di utilizzare goniometri, calcolatrici, software e app per facilitare il processo.
• Comprendi i concetti: Non limitarti a memorizzare formule; cerca di capire la logica dietro di esse.
• Visualizza il problema: Disegna sempre un diagramma per visualizzare l'angolo e le relazioni geometriche coinvolte.
• Controlla i tuoi risultati: Verifica sempre che la tua risposta sia ragionevole e coerente con le informazioni che hai a disposizione.

Con impegno e perseveranza, sarai in grado di padroneggiare l'arte di misurare gli angoli e di applicare questa conoscenza in una vasta gamma di contesti, dalla matematica alla fisica, dall'ingegneria all'architettura.