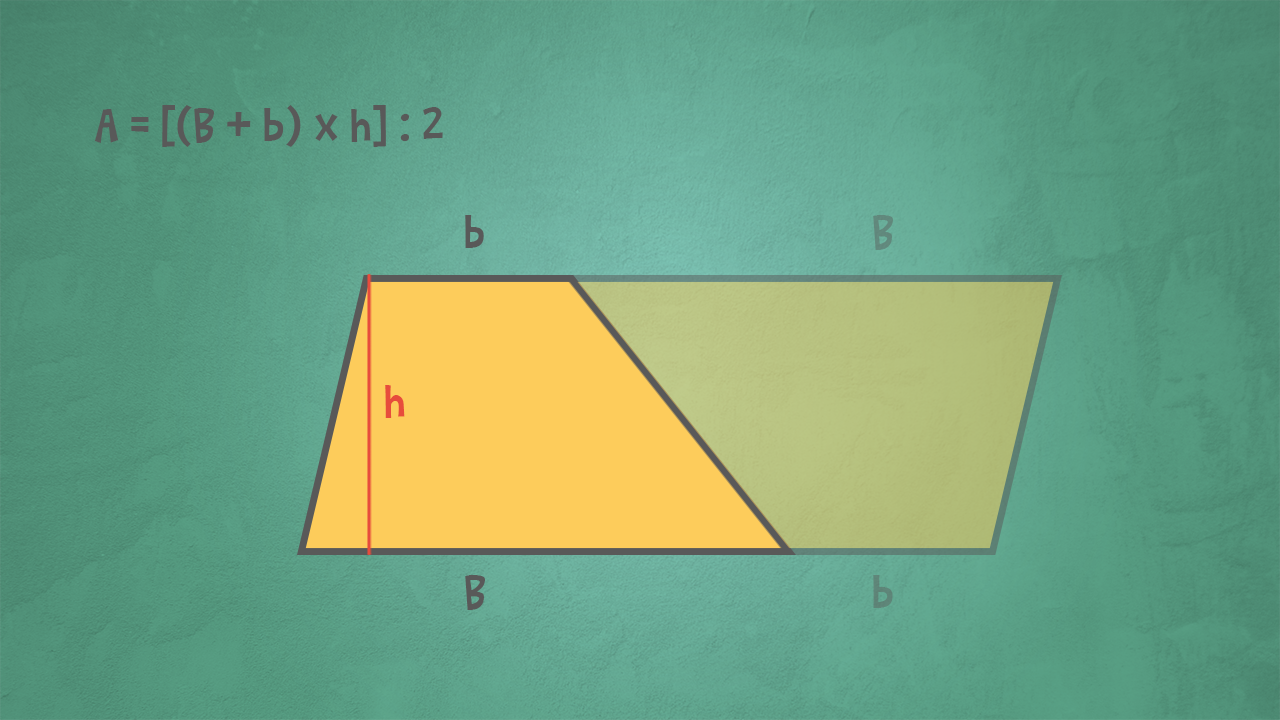Come Calcolare L Area Del Trapezio
Ciao a tutti! A volte, la matematica può sembrare un viaggio attraverso un labirinto intricato, pieno di formule e concetti che ci sfidano. Ma, se ci avviciniamo con curiosità e un pizzico di umiltà, scopriamo che ogni singolo concetto è una porta verso una comprensione più profonda del mondo che ci circonda. Oggi, esploriamo insieme un'area specifica di questo affascinante territorio: il trapezio e come calcolarne l'area.
Il Trapezio: Una Figura Versatile
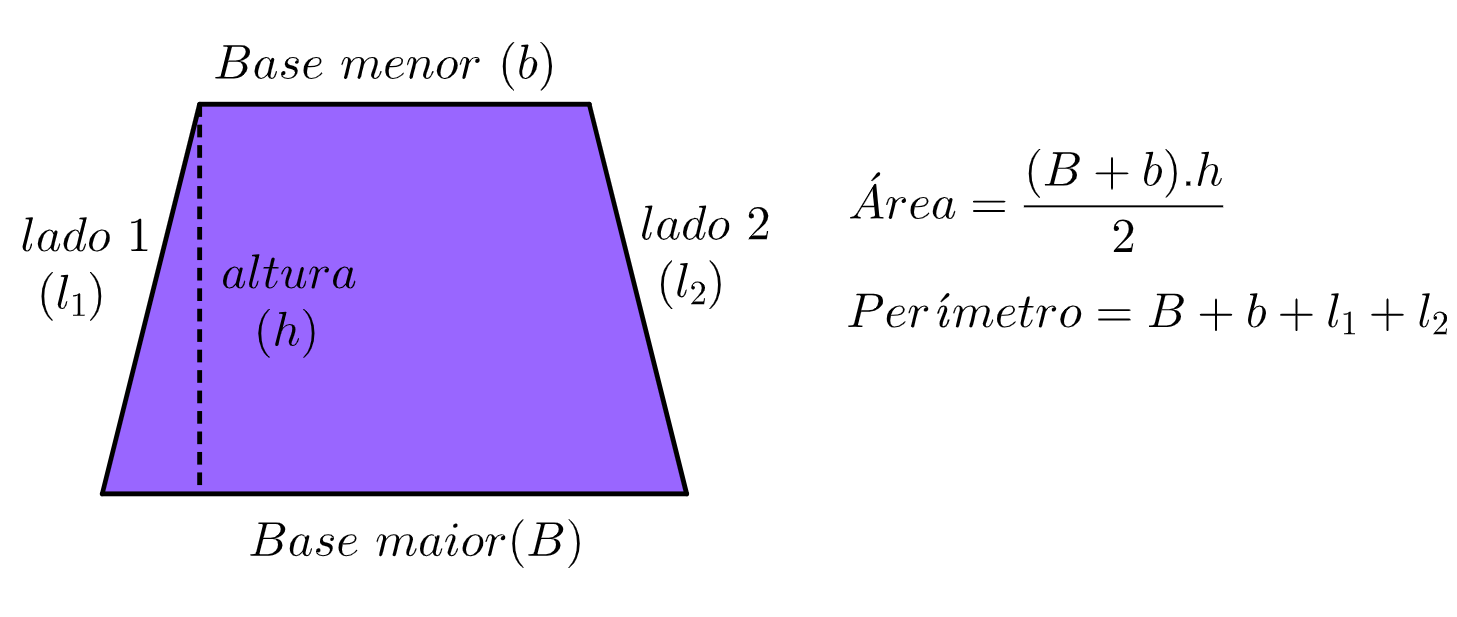
Il trapezio, con le sue due basi parallele e i lati obliqui, è una figura geometrica che incontriamo spesso nella vita di tutti i giorni, magari senza accorgercene. Pensate alla forma di una borsa, al tetto di una casetta stilizzata, o persino a certe fette di torta! Capire come calcolarne l'area, quindi, non è solo un esercizio teorico, ma uno strumento pratico che ci permette di interpretare e interagire meglio con il nostro ambiente.
Un Approccio Graduale
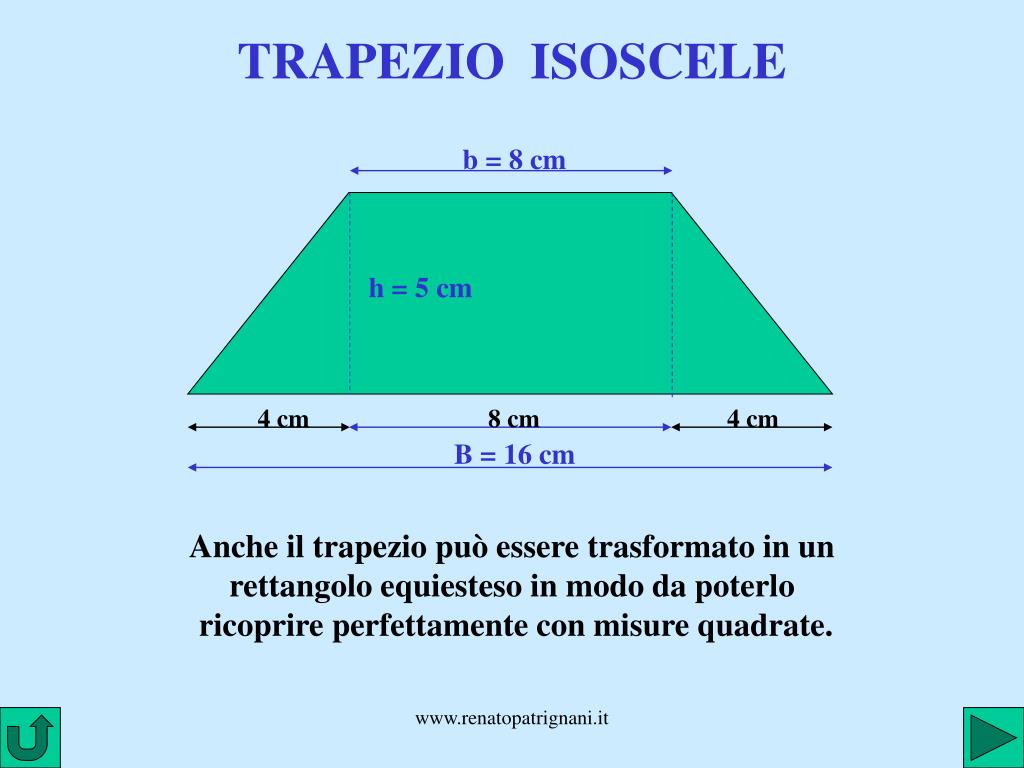
Immaginate di avere un trapezio. La sua bellezza sta nella sua irregolarità controllata. Per calcolarne l'area, partiamo da un'idea fondamentale: scomporre il complesso in semplice. Possiamo visualizzare il trapezio come la combinazione di figure più familiari, come rettangoli e triangoli. Questa scomposizione ci aiuta a "vedere" la formula che andremo a utilizzare.
La formula, in realtà, è un'elegante sintesi di questo processo di scomposizione. Si presenta così:
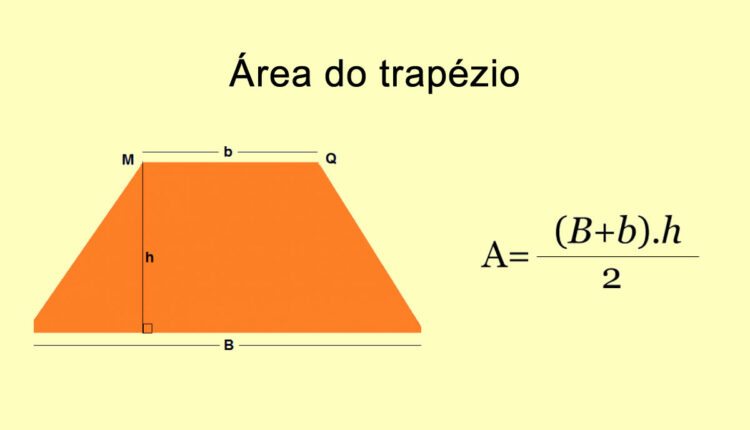
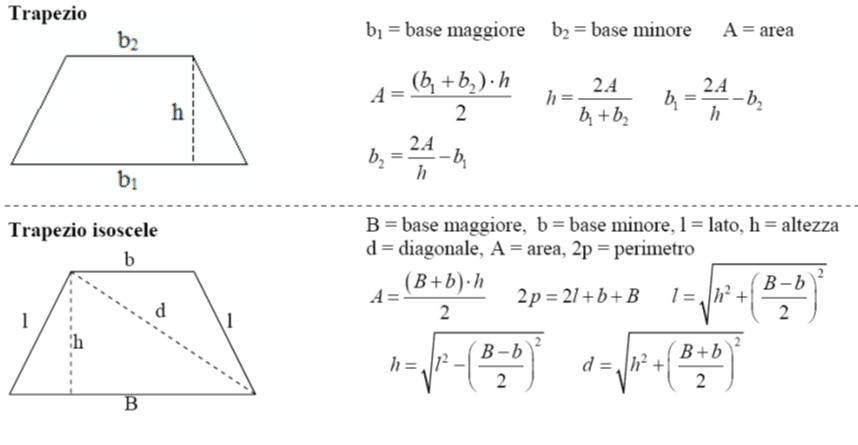
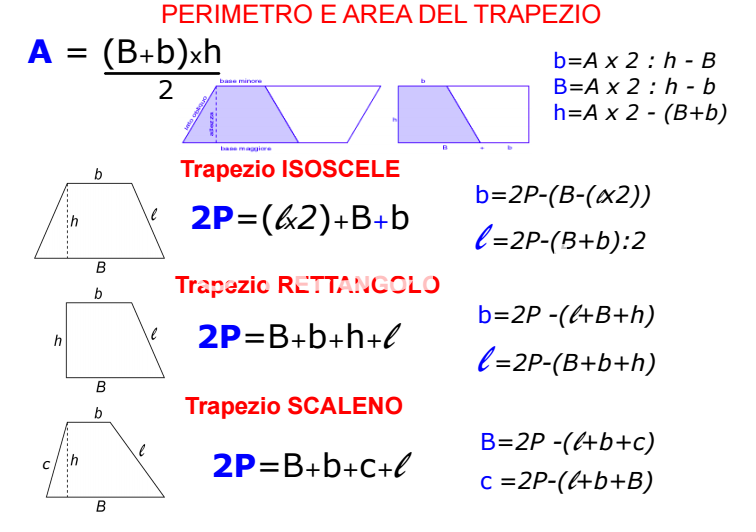
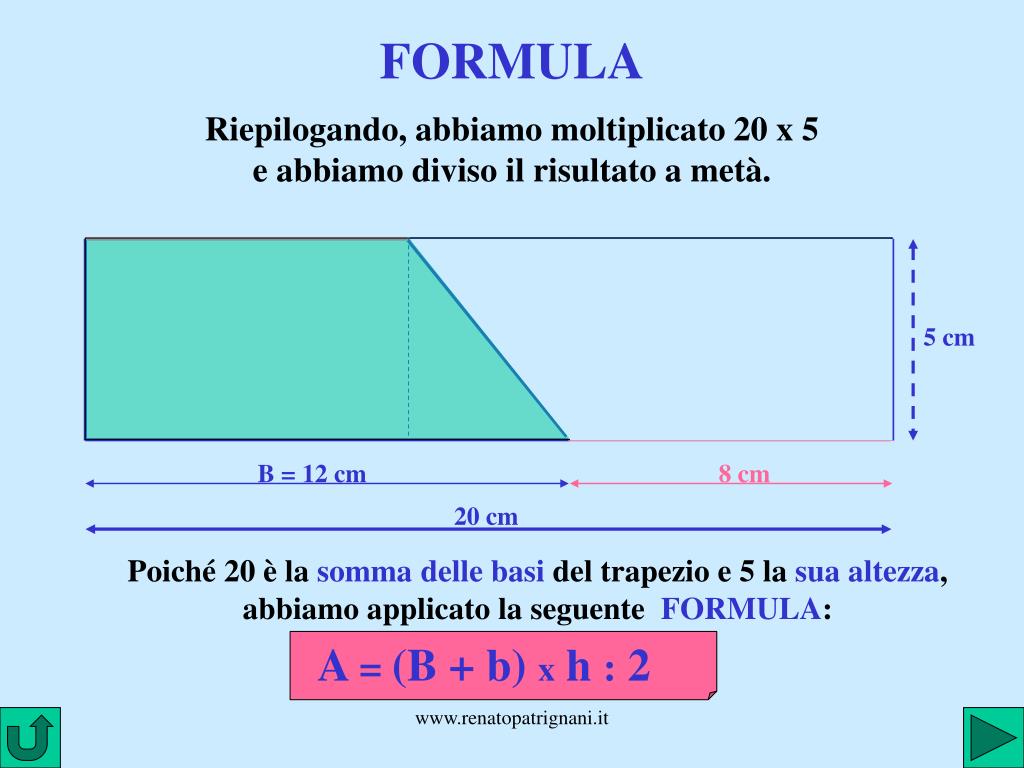
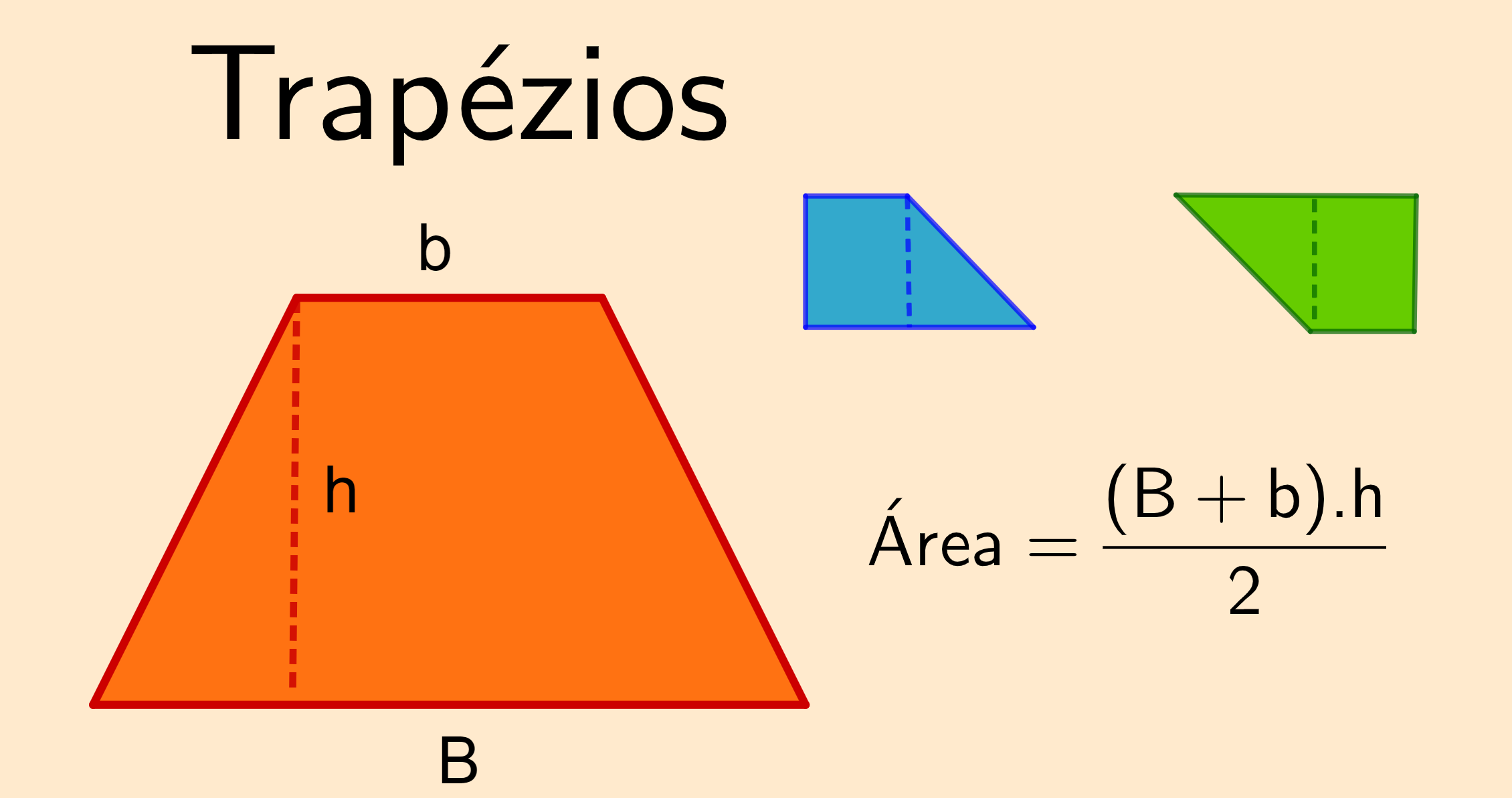
Area = (Base maggiore + Base minore) * Altezza / 2
Dove:
- Base maggiore è il lato più lungo del trapezio.
- Base minore è il lato parallelo più corto.
- Altezza è la distanza perpendicolare tra le due basi.
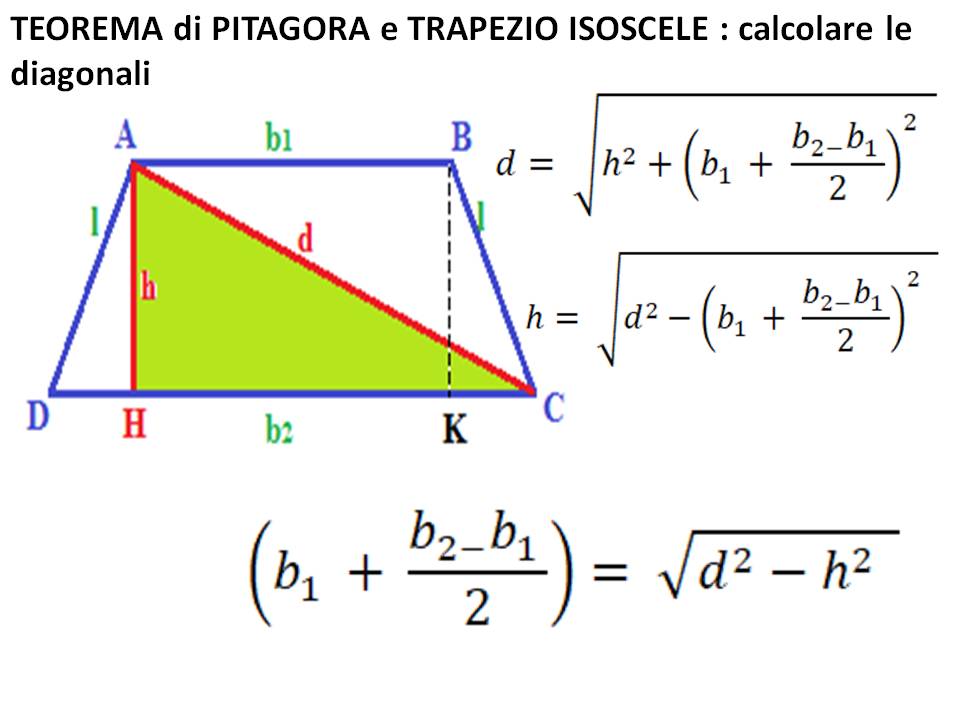
Notate come la formula riflette la nostra intuizione. Sommiamo le due basi, che rappresentano una sorta di "media" della larghezza del trapezio, e moltiplichiamo per l'altezza. Dividiamo per due, perché stiamo considerando una figura che è, in un certo senso, "metà" di un parallelogramma costruito a partire dal trapezio stesso.
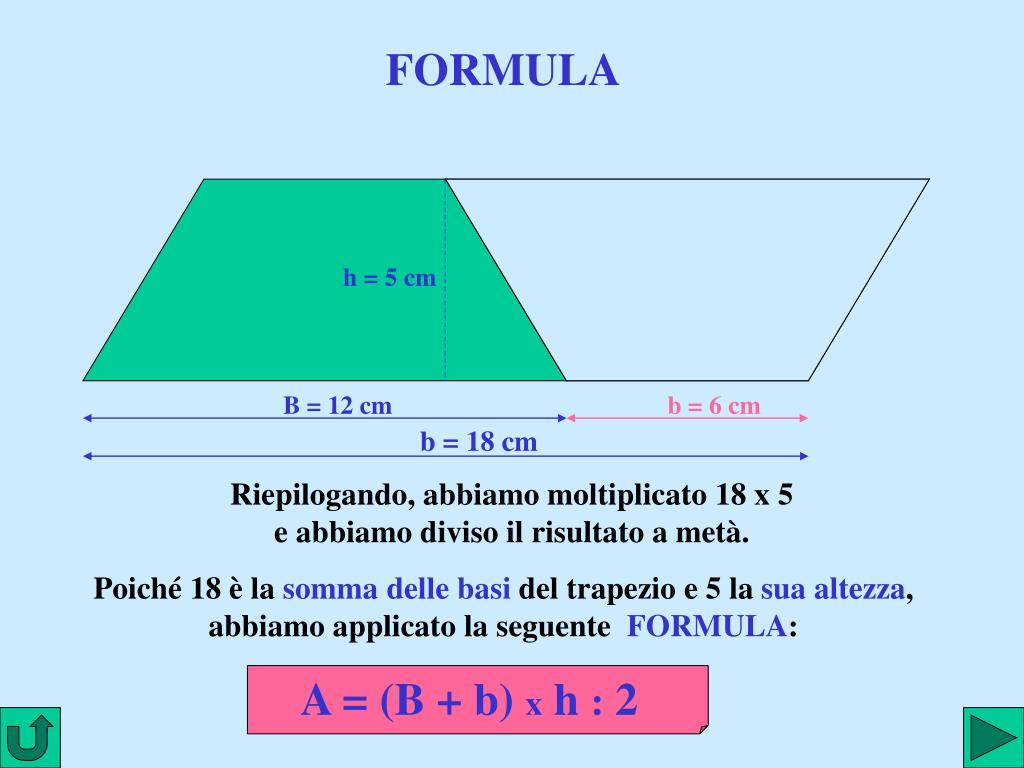
Proviamo a rendere questo concetto ancora più tangibile. Immaginate di avere un trapezio ritagliato in un foglio di carta. Ora, ritagliate un altro trapezio identico. Ruotate il secondo trapezio di 180 gradi e accostatelo al primo, in modo che le basi maggiori e minori si tocchino. Avrete formato un parallelogramma! L'area di questo parallelogramma è data dalla somma delle basi del trapezio originale moltiplicata per l'altezza. Poiché il parallelogramma è composto da due trapezi identici, l'area di un singolo trapezio è la metà dell'area del parallelogramma.
Oltre la Formula: Coltivare la Comprensione
Ricordate, la matematica non è solo memorizzare formule, ma comprendere il ragionamento che le sostiene. Incoraggiatevi a sperimentare, a disegnare trapezi di diverse forme e dimensioni, a calcolarne l'area e a verificare i risultati. Non abbiate paura di sbagliare; gli errori sono opportunità preziose per imparare e crescere. Ogni errore è un passo avanti verso una comprensione più solida.
La bellezza della matematica risiede nella sua universalità e nella sua capacità di svelare i segreti del mondo. Continuate a esplorare con curiosità, ad affrontare le sfide con perseveranza e ad accogliere la conoscenza con umiltà. Ogni nuovo concetto che imparate è una tessera di un mosaico sempre più grande, che vi permette di vedere il mondo con occhi nuovi e di apprezzarne la sua straordinaria complessità.
Forza, il mondo della matematica vi aspetta! E ricordate, ogni passo, anche il più piccolo, è un progresso.