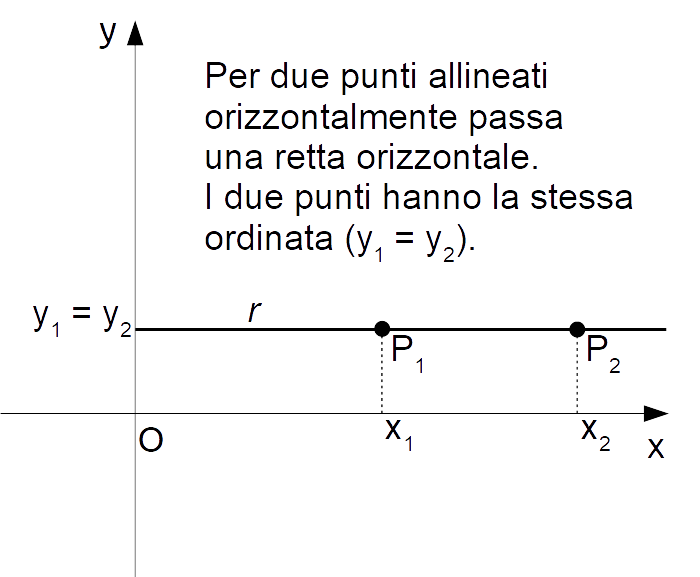Coefficiente Angolare Di Una Retta Passante Per Due Punti

Il coefficiente angolare, spesso indicato con la lettera m, è un concetto fondamentale nella geometria analitica che descrive l'inclinazione di una retta rispetto all'asse delle ascisse (l'asse x) in un sistema di coordinate cartesiane. Comprendere come calcolarlo quando si conoscono due punti sulla retta è essenziale per diverse applicazioni in matematica, fisica, ingegneria e altre discipline.

Calcolo del Coefficiente Angolare

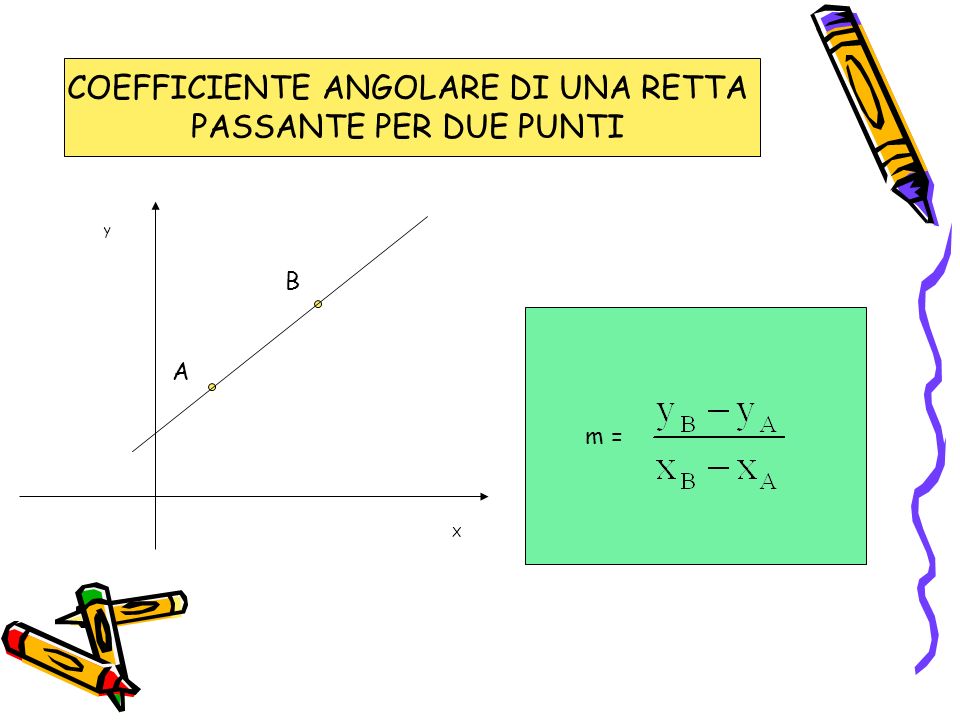
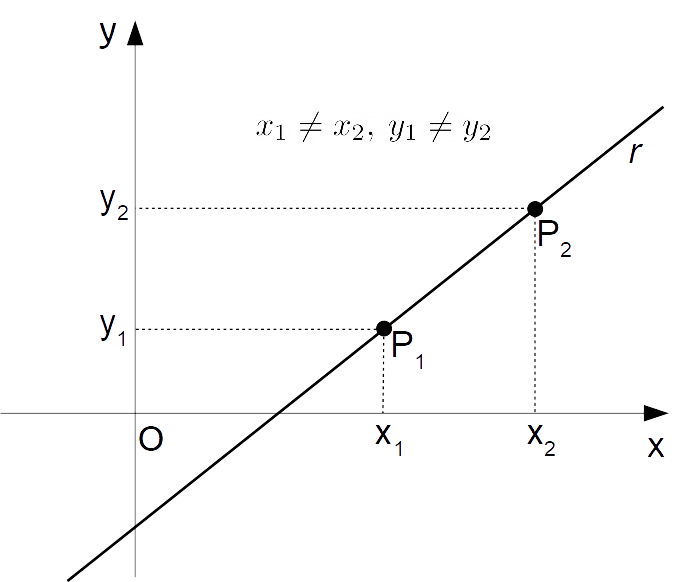
Il coefficiente angolare di una retta che passa per due punti dati, A(x₁, y₁) e B(x₂, y₂), si calcola con la seguente formula:

m = (y₂ - y₁) / (x₂ - x₁)

Questa formula rappresenta la variazione verticale (differenza tra le ordinate, y) divisa per la variazione orizzontale (differenza tra le ascisse, x). È importante notare che l'ordine in cui si sottraggono le coordinate deve essere coerente: se si fa (y₂ - y₁) al numeratore, si deve fare (x₂ - x₁) al denominatore.

Interpretazione Geometrica

Il coefficiente angolare m fornisce informazioni cruciali sull'inclinazione e la direzione della retta:

m > 0: La retta è crescente. Man mano che ci si sposta da sinistra a destra lungo la retta, i valori di y aumentano. Più grande è m, più ripida è la retta.
m < 0: La retta è decrescente. Man mano che ci si sposta da sinistra a destra lungo la retta, i valori di y diminuiscono. Più piccolo è m (cioè, più grande è il suo valore assoluto), più ripida è la retta (in discesa).
m = 0: La retta è orizzontale. Tutti i punti sulla retta hanno la stessa ordinata (y), e quindi la variazione verticale è zero.
m non definito: La retta è verticale. Tutti i punti sulla retta hanno la stessa ascissa (x), e quindi la variazione orizzontale è zero. La divisione per zero non è definita, quindi il coefficiente angolare non esiste.

Considerazioni Importanti

È fondamentale prestare attenzione ai seguenti aspetti quando si calcola il coefficiente angolare:

Ordine dei punti: Come menzionato prima, l'ordine in cui si sottraggono le coordinate deve essere mantenuto coerente sia al numeratore che al denominatore. Se si inverte l'ordine in entrambi, il risultato sarà lo stesso (il segno si semplifica).
Rette verticali: Il coefficiente angolare non è definito per le rette verticali. In questo caso, si dice che la retta ha pendenza infinita, anche se tecnicamente non è un valore numerico. La sua equazione è del tipo x = costante.
Rette orizzontali: Il coefficiente angolare di una retta orizzontale è sempre zero. La sua equazione è del tipo y = costante.
Rette parallele: Due rette sono parallele se e solo se hanno lo stesso coefficiente angolare.
Rette perpendicolari: Due rette sono perpendicolari se e solo se il prodotto dei loro coefficienti angolari è -1. Se la retta 1 ha coefficiente angolare m₁ e la retta 2 ha coefficiente angolare m₂, allora m₁ * m₂ = -1. In alternativa, il coefficiente angolare di una retta perpendicolare a una retta con coefficiente angolare *m* è -1/*m*.

Esempi Pratici

Vediamo alcuni esempi per illustrare come calcolare il coefficiente angolare:

Esempio 1: Calcolare il coefficiente angolare della retta passante per i punti A(1, 2) e B(4, 8).

Soluzione:

m = (8 - 2) / (4 - 1) = 6 / 3 = 2

La retta ha un coefficiente angolare di 2, quindi è crescente.

Esempio 2: Calcolare il coefficiente angolare della retta passante per i punti C(-2, 5) e D(3, -1).

Soluzione:

m = (-1 - 5) / (3 - (-2)) = -6 / 5 = -1.2

La retta ha un coefficiente angolare di -1.2, quindi è decrescente.

Esempio 3: Calcolare il coefficiente angolare della retta passante per i punti E(2, 3) e F(2, 7).

Soluzione:

m = (7 - 3) / (2 - 2) = 4 / 0 (Non definito)

La retta è verticale e il suo coefficiente angolare non è definito.

Applicazioni nel Mondo Reale

Il concetto di coefficiente angolare ha numerose applicazioni pratiche. Eccone alcuni:

Ingegneria Civile: Gli ingegneri utilizzano il coefficiente angolare per calcolare la pendenza delle strade, dei tetti e di altre strutture. Una pendenza corretta è essenziale per garantire il drenaggio dell'acqua e la stabilità strutturale. Ad esempio, la pendenza di una rampa per disabili deve rispettare normative precise per garantire l'accessibilità.
Fisica: In fisica, il coefficiente angolare può rappresentare la velocità di un oggetto in un grafico posizione-tempo o l'accelerazione in un grafico velocità-tempo.
Economia: In economia, il coefficiente angolare può rappresentare il costo marginale di produzione (la variazione del costo totale al variare della quantità prodotta).
Statistica: Nella regressione lineare, il coefficiente angolare rappresenta la variazione prevista della variabile dipendente per ogni unità di variazione della variabile indipendente. Ad esempio, in uno studio che mette in relazione il numero di ore di studio e il voto ad un esame, il coefficiente angolare della retta di regressione indica di quanto aumenta in media il voto per ogni ora di studio aggiuntiva.
Grafica Computerizzata: Il coefficiente angolare è utilizzato per calcolare la direzione e l'inclinazione delle linee e delle superfici nella grafica 3D.
Navigazione: In cartografia e navigazione, il coefficiente angolare può essere utilizzato per determinare la pendenza di un terreno o la direzione di una rotta.

Esempio Dati Reali: Andamento Azionario

Consideriamo l'andamento del prezzo di un'azione. Supponiamo di avere i seguenti dati:

Giorno 1: Prezzo = €10
Giorno 5: Prezzo = €12

Possiamo rappresentare questi dati come due punti: A(1, 10) e B(5, 12). Il coefficiente angolare della retta che connette questi due punti rappresenta la variazione media del prezzo dell'azione per giorno:

m = (12 - 10) / (5 - 1) = 2 / 4 = 0.5

Questo significa che, in media, il prezzo dell'azione è aumentato di €0.5 al giorno in quel periodo. Ovviamente, questo è solo un'approssimazione lineare e non tiene conto delle fluttuazioni giornaliere, ma fornisce una visione generale del trend.

Conclusioni

Il coefficiente angolare è uno strumento potente e versatile per analizzare le rette e le loro proprietà. La sua comprensione è fondamentale per affrontare problemi in diverse aree della matematica e delle scienze applicate. Sapere come calcolarlo a partire da due punti è una competenza di base che apre la strada a concetti più avanzati come le derivate, le equazioni differenziali e l'analisi di dati.

Invito all'azione: Esercitati con diversi esempi per familiarizzare con il calcolo del coefficiente angolare e le sue interpretazioni geometriche. Considera come questo concetto può essere applicato ai tuoi campi di interesse e cerca esempi reali per rafforzare la tua comprensione. Approfondisci lo studio della geometria analitica per scoprire ulteriori applicazioni e collegamenti con altri concetti matematici.