Classificazione Triangoli In Base Agli Angoli

Ti sei mai chiesto come mai alcuni triangoli sembrano più "appuntiti" di altri? O perché alcuni sono perfetti per costruire una rampa, mentre altri no? La risposta sta nella classificazione dei triangoli in base ai loro angoli! Capire questa classificazione non è solo teoria geometrica; è uno strumento potente per risolvere problemi pratici e apprezzare meglio il mondo che ci circonda. Molti studenti trovano la geometria inizialmente ostica, ma rompere le barriere con una spiegazione chiara e esempi concreti può rendere l'apprendimento piacevole e proficuo.
La Definizione Fondamentale di Triangolo
Prima di addentrarci nella classificazione, ricapitoliamo cosa è un triangolo. Un triangolo è una figura geometrica piana delimitata da tre lati e, di conseguenza, ha tre angoli interni. La somma degli angoli interni di qualsiasi triangolo è sempre 180 gradi. Questa è una regola aurea che non cambia mai, indipendentemente dalla forma del triangolo!
Immagina un triangolo come una torta divisa in tre fette: la somma delle tre fette deve sempre equivalere all'intera torta (180 gradi). Questa semplice analogia può aiutarti a ricordare questo principio fondamentale.
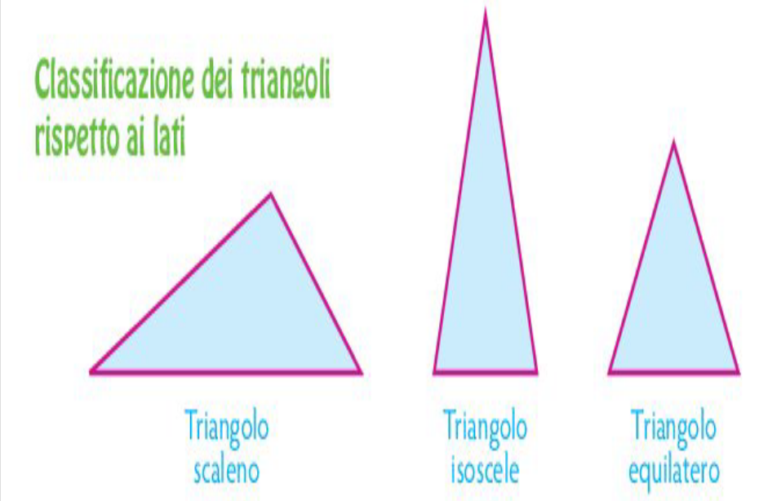
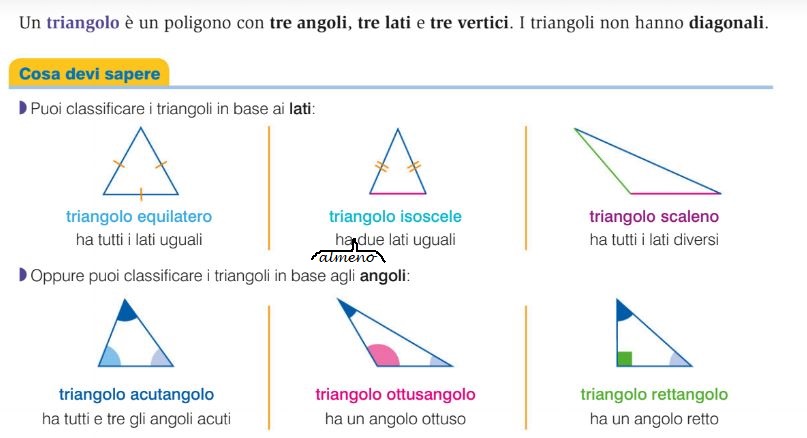
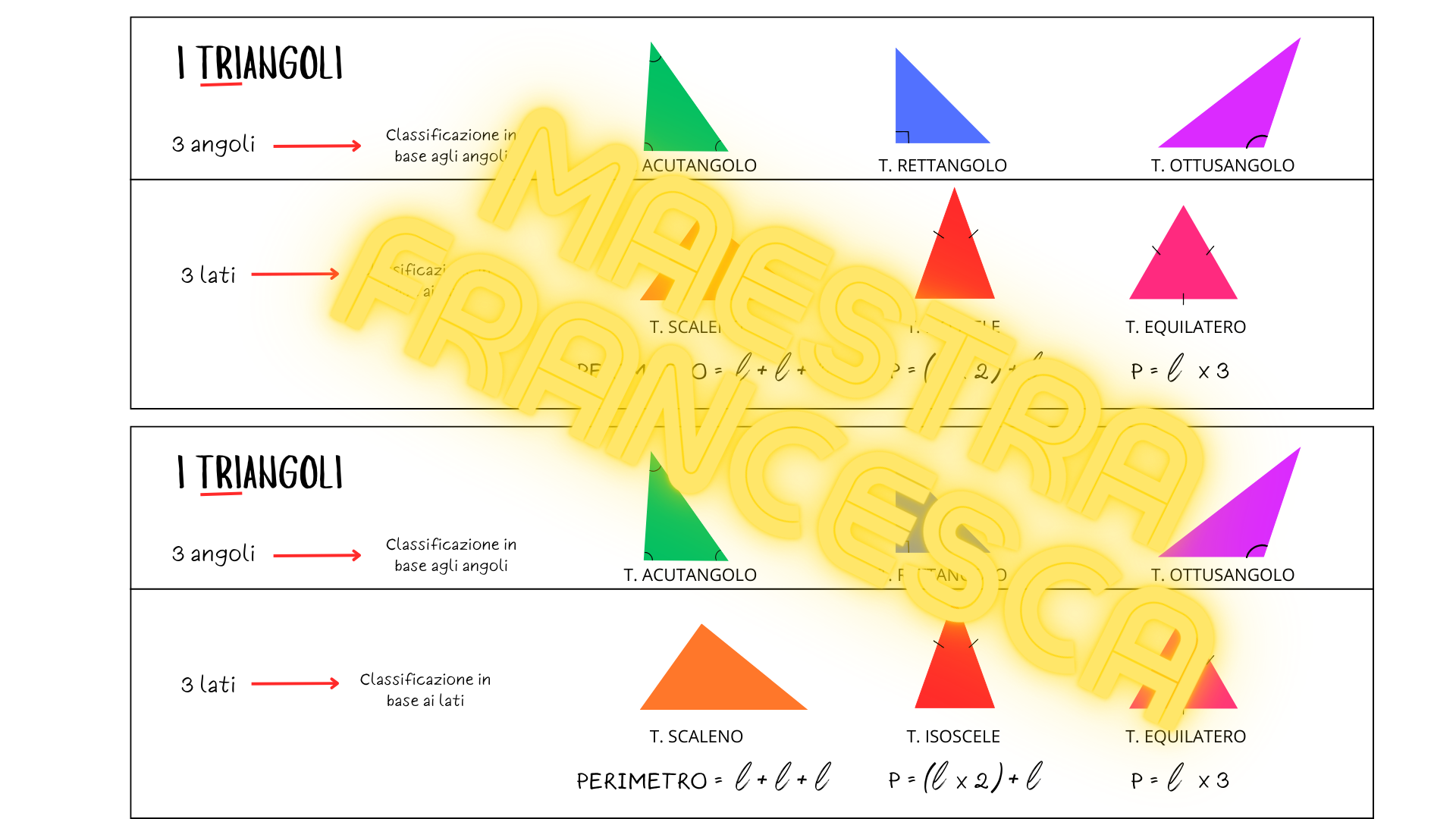
Classificazione in Base agli Angoli: Acutangolo, Rettangolo, Ottusangolo
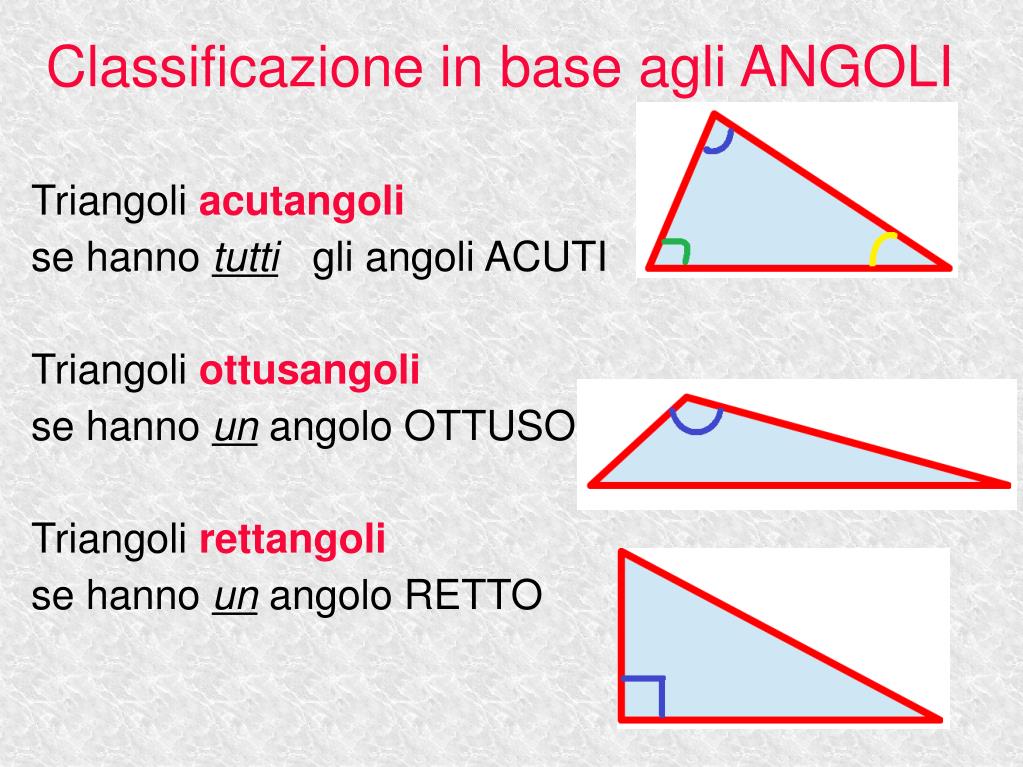
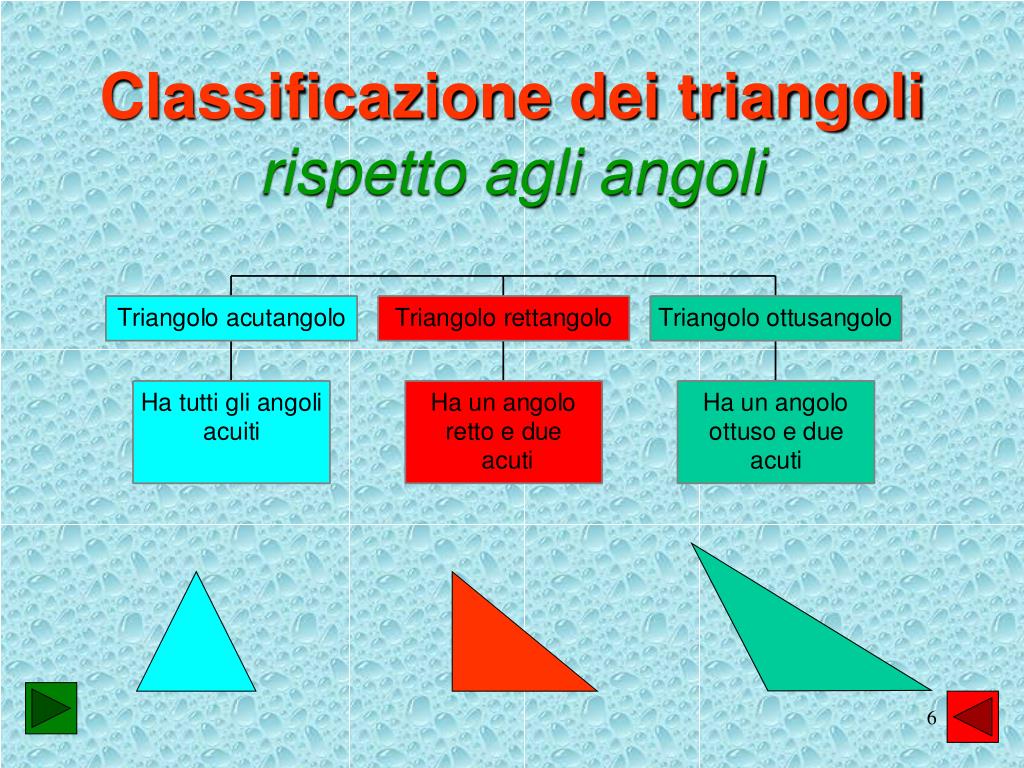
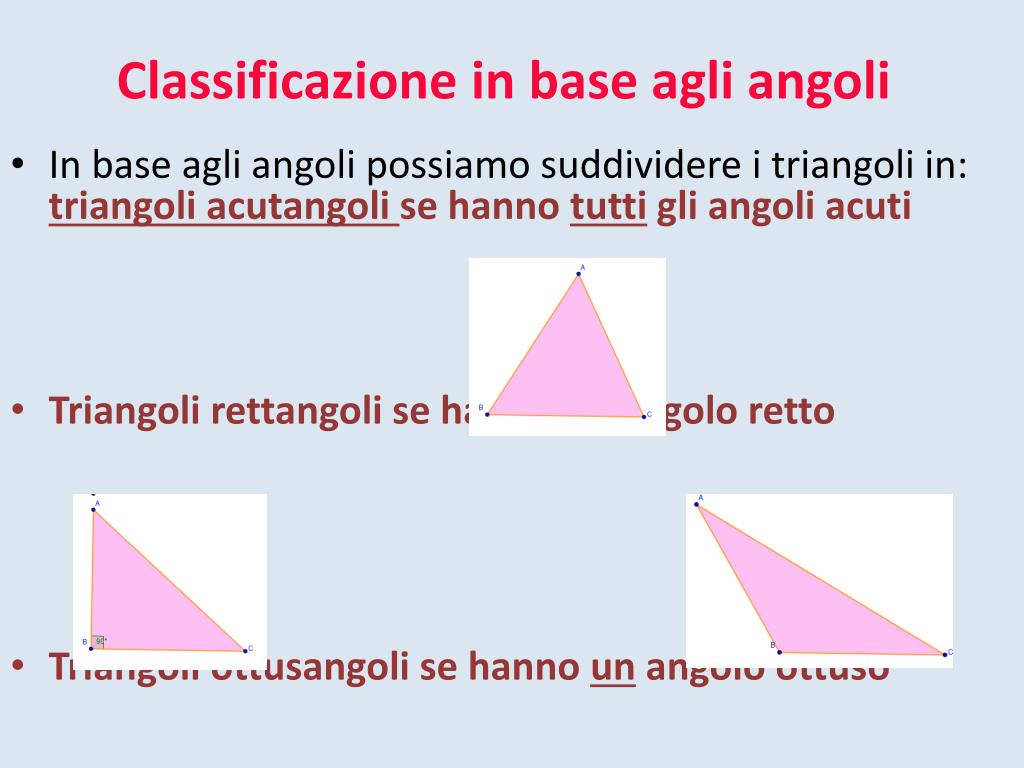
La classificazione dei triangoli in base agli angoli si basa sulla misurazione dei loro angoli interni. Ci sono tre categorie principali:
Triangolo Acutangolo
Un triangolo acutangolo è un triangolo in cui tutti e tre gli angoli interni sono acuti, ovvero minori di 90 gradi. Pensa a un triangolo acutangolo come a un triangolo "amichevole" dove nessun angolo è troppo grande o "aggressivo".
Esempio pratico: un triangolo equilatero (con tutti i lati uguali) è sempre un triangolo acutangolo, poiché tutti i suoi angoli misurano 60 gradi.
Triangolo Rettangolo
Un triangolo rettangolo è un triangolo in cui uno degli angoli interni è retto, ovvero misura esattamente 90 gradi. L'angolo retto è spesso indicato con un piccolo quadrato nell'angolo stesso.
Esempio pratico: L'angolo di una porta standard rispetto al muro è un angolo retto. Molti oggetti che ci circondano utilizzano angoli retti per garantire stabilità e funzionalità.
Il lato opposto all'angolo retto è chiamato ipotenusa ed è sempre il lato più lungo del triangolo rettangolo. Gli altri due lati sono chiamati cateti. Il teorema di Pitagora, un pilastro della geometria, si applica esclusivamente ai triangoli rettangoli: a² + b² = c², dove a e b sono i cateti e c è l'ipotenusa.
Triangolo Ottusangolo
Un triangolo ottusangolo è un triangolo in cui uno degli angoli interni è ottuso, ovvero maggiore di 90 gradi ma minore di 180 gradi. In altre parole, questo triangolo ha un angolo "spalancato".
Esempio pratico: Immagina una fetta di pizza particolarmente grande; l'angolo della punta potrebbe essere ottuso.
Importante: Un triangolo può avere solo un angolo ottuso. Se avesse due angoli ottusi, la somma degli angoli interni supererebbe i 180 gradi, violando la regola fondamentale dei triangoli.
Perché è Importante la Classificazione?
La classificazione dei triangoli in base agli angoli non è solo un esercizio teorico; ha importanti applicazioni pratiche in molti campi:
- Architettura e Ingegneria: Gli architetti e gli ingegneri utilizzano i triangoli per progettare strutture stabili e resistenti. I triangoli rettangoli, in particolare, sono fondamentali per la costruzione di ponti, edifici e altre infrastrutture. La stabilità di un triangolo deriva dalla sua rigidità: una volta fissati i lati, la forma del triangolo è univocamente determinata.
- Navigazione: I navigatori utilizzano la trigonometria, che si basa sui principi dei triangoli rettangoli, per determinare la posizione e la direzione.
- Grafica e Design: I triangoli sono elementi essenziali nel design grafico e nella modellazione 3D. La loro forma e orientamento influenzano l'estetica e la funzionalità di un progetto.
- Fisica: La decomposizione di forze in componenti ortogonali (perpendicolari) si basa sull'utilizzo di triangoli rettangoli.
Come Identificare i Triangoli in Base agli Angoli
Ecco alcuni consigli pratici per identificare i triangoli in base ai loro angoli:
- Misura gli Angoli: Il modo più preciso è utilizzare un goniometro per misurare gli angoli interni del triangolo.
- Osserva gli Angoli: Se non hai un goniometro, cerca angoli retti (identificabili dal piccolo quadrato nell'angolo). Se vedi un angolo retto, hai un triangolo rettangolo. Se tutti gli angoli sembrano "stretti" (minori di 90 gradi), hai un triangolo acutangolo. Se vedi un angolo "spalancato" (maggiore di 90 gradi), hai un triangolo ottusangolo.
- Utilizza le Proprietà dei Triangoli: Ricorda che la somma degli angoli interni di un triangolo è sempre 180 gradi. Se conosci due angoli, puoi calcolare il terzo e determinare la classificazione del triangolo.
Esercizi Pratici
Per mettere alla prova la tua comprensione, prova a identificare la classificazione dei seguenti triangoli in base agli angoli (senza usare un goniometro, se possibile):
- Un triangolo con angoli di 30, 60 e 90 gradi: Triangolo Rettangolo
- Un triangolo con angoli di 45, 45 e 90 gradi: Triangolo Rettangolo (inoltre, è anche isoscele)
- Un triangolo con angoli di 60, 60 e 60 gradi: Triangolo Acutangolo (inoltre, è anche equilatero)
- Un triangolo con angoli di 20, 30 e 130 gradi: Triangolo Ottusangolo
- Un triangolo con angoli di 50, 70 e 60 gradi: Triangolo Acutangolo
Conclusione
La classificazione dei triangoli in base agli angoli è un concetto fondamentale della geometria che ha applicazioni pratiche in molti campi. Comprendere le differenze tra triangoli acutangoli, rettangoli e ottusangoli ti permette di analizzare e risolvere problemi geometrici con maggiore sicurezza e precisione. Non dimenticare che la pratica costante e l'applicazione dei concetti in situazioni reali sono la chiave per padroneggiare la geometria e apprezzare la bellezza delle forme che ci circondano. Non aver paura di sperimentare, disegnare triangoli di diverse forme e misurare i loro angoli. La geometria è un mondo affascinante che aspetta solo di essere esplorato!