Centro Del Fascio Di Rette Formula

Il concetto di fascio di rette è fondamentale nella geometria analitica, offrendo un metodo potente per descrivere insiemi infiniti di rette che condividono una proprietà comune. Capire il Centro del Fascio di Rette e la relativa formula è cruciale per risolvere una varietà di problemi geometrici e algebrici. In questo articolo, esploreremo in dettaglio il fascio di rette, concentrandoci sulla sua formula e le sue applicazioni pratiche.

Comprendere il Fascio di Rette

Un fascio di rette, in termini semplici, è un insieme infinito di rette che condividono una caratteristica specifica. Questa caratteristica può essere un punto comune, una direzione comune (rette parallele), o una combinazione di vincoli geometrici. Esistono principalmente due tipi di fasci di rette:

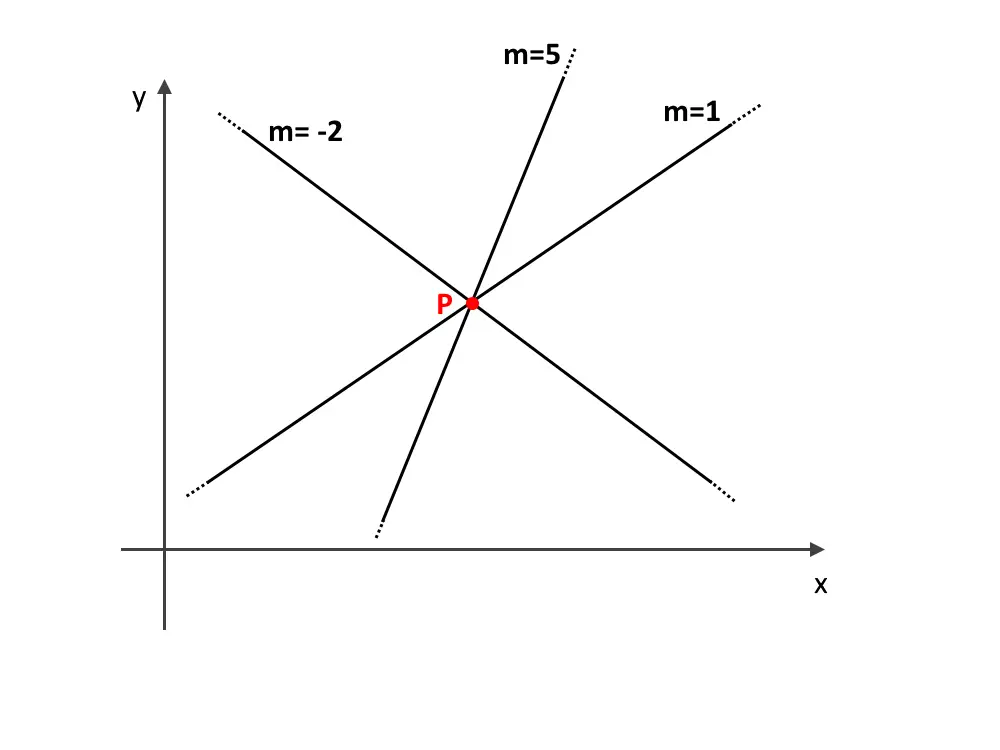
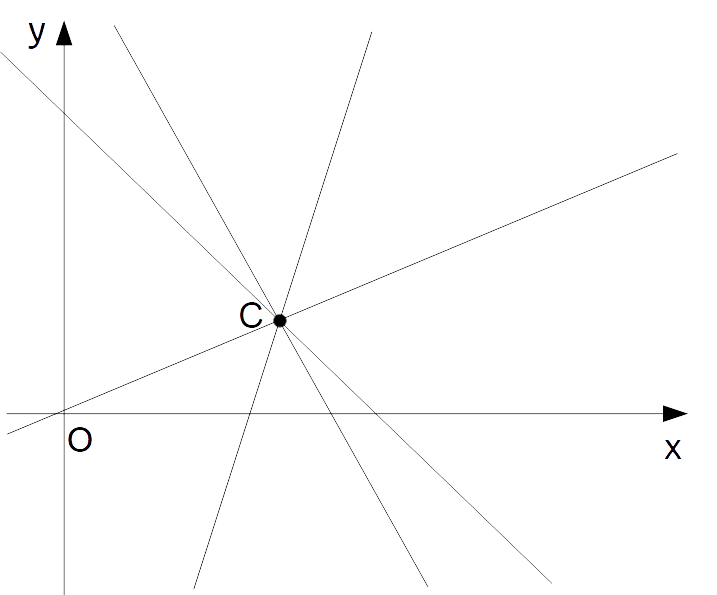
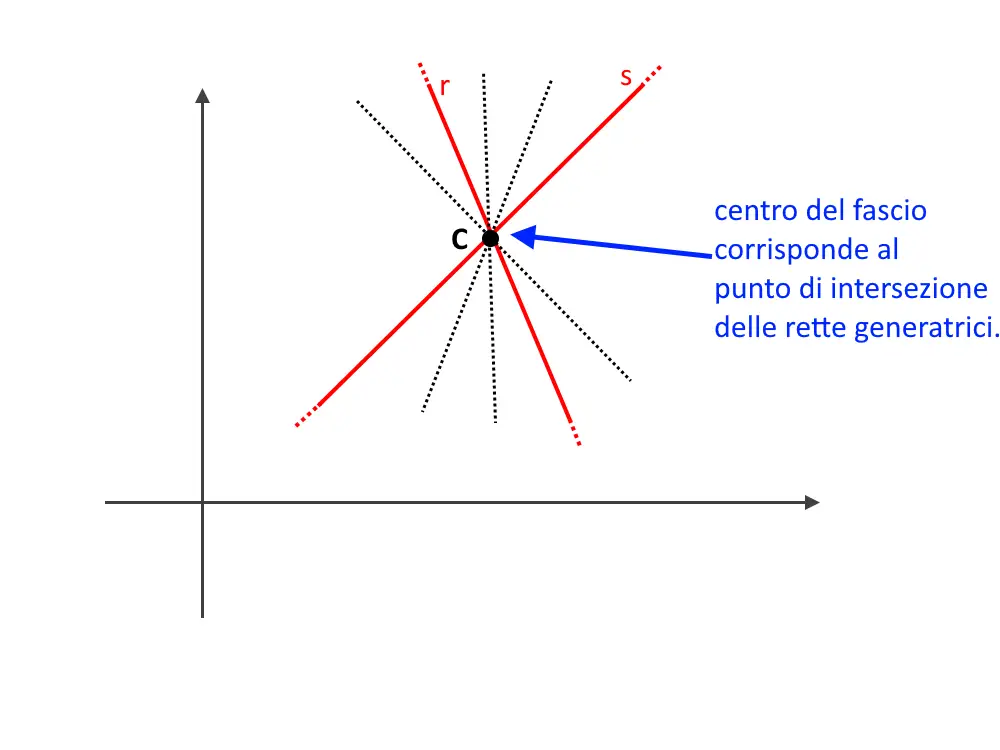
Fascio di Rette Proprio

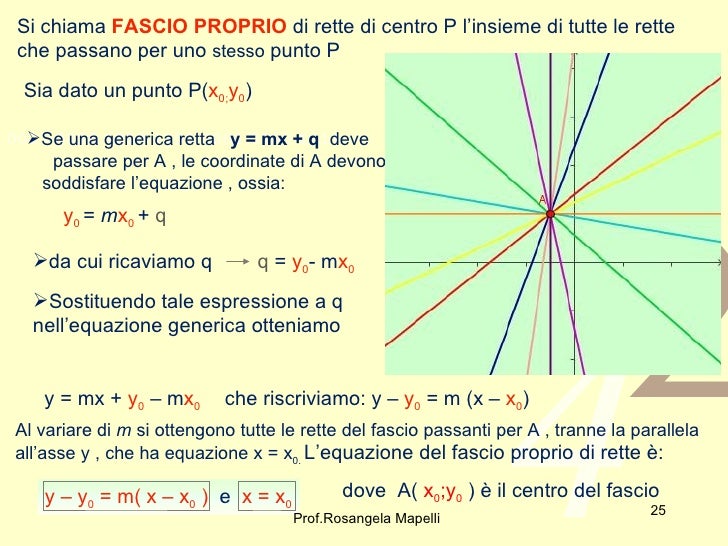
Un fascio di rette proprio è un insieme di rette che passano tutte per lo stesso punto, chiamato il centro del fascio. Questo centro è il punto di intersezione di tutte le rette nel fascio. La formula generale per un fascio di rette proprio è data dalla combinazione lineare di due rette che si intersecano in quel punto:

a(Ax + By + C) + b(Dx + Ey + F) = 0

Dove:

• Ax + By + C = 0 e Dx + Ey + F = 0 sono le equazioni di due rette distinte che si intersecano.
• a e b sono parametri reali. Variando a e b, si ottengono tutte le rette del fascio.

È fondamentale comprendere che il rapporto tra a e b determina l'inclinazione della retta nel fascio. Quando uno dei due parametri è zero, si ottiene una delle due rette generatrici.

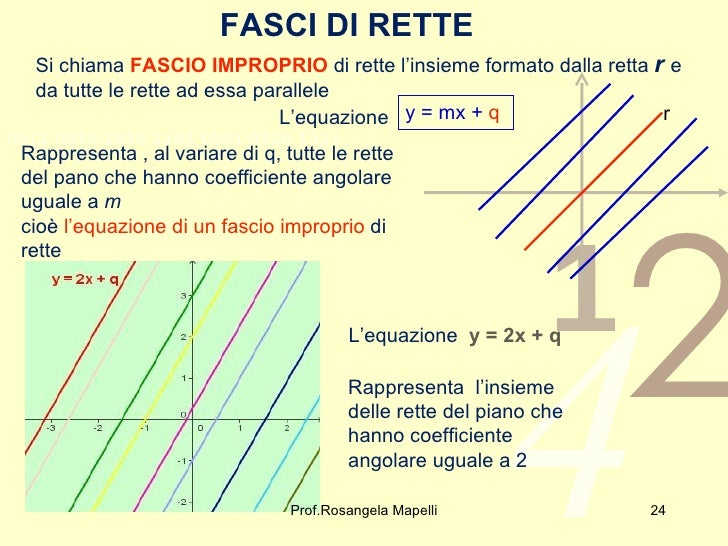
Fascio di Rette Improprio

Un fascio di rette improprio è un insieme di rette parallele. In questo caso, non esiste un centro del fascio nel piano euclideo (il centro è idealmente all'infinito). La formula generale per un fascio di rette improprio è:

y = mx + q

Dove:

• m è la pendenza comune a tutte le rette del fascio (è costante).
• q è un parametro reale che varia, determinando la traslazione verticale della retta.

In questo caso, tutte le rette hanno la stessa pendenza e differiscono solo per l'intercetta con l'asse y.

La Formula del Centro del Fascio di Rette Proprio

Come abbiamo detto, il centro del fascio è il punto cruciale per un fascio di rette proprio. Trovare le coordinate di questo punto è essenziale per risolvere molti problemi. Per determinare il centro del fascio, dobbiamo risolvere il sistema di equazioni formato dalle due rette generatrici:

{ Ax + By + C = 0 { Dx + Ey + F = 0

Risolvendo questo sistema (ad esempio, con il metodo di sostituzione, eliminazione o Cramer), si ottengono le coordinate (x₀, y₀) del centro del fascio. Queste coordinate soddisfano entrambe le equazioni delle rette generatrici.

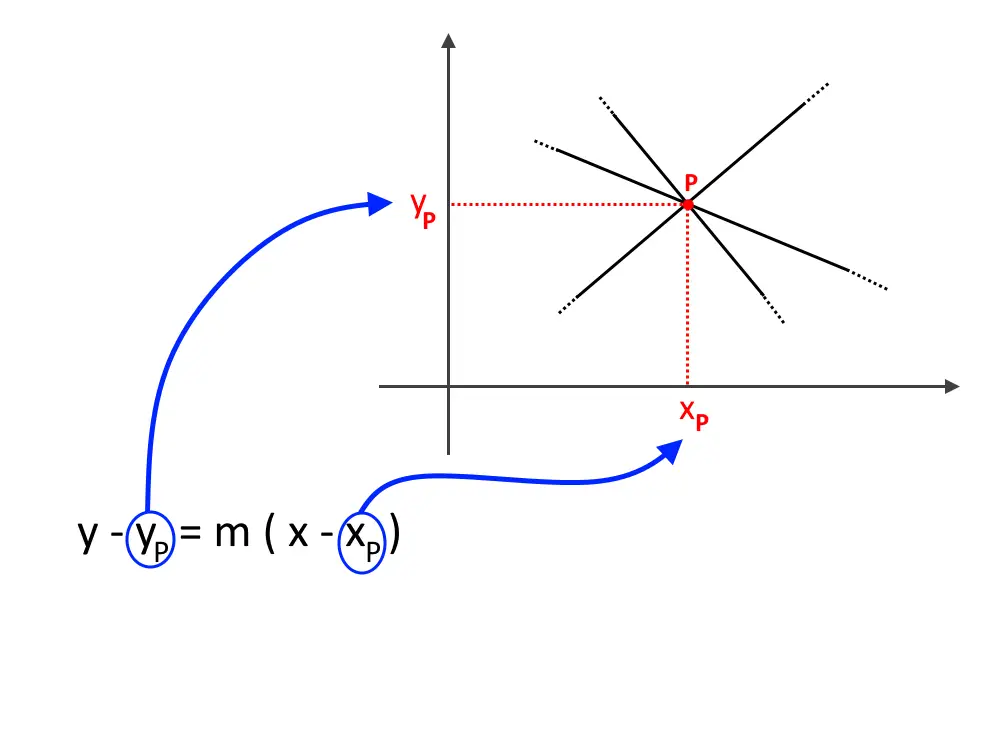
Una volta trovate le coordinate (x₀, y₀), è possibile scrivere l'equazione del fascio in una forma alternativa, spesso utile per risolvere problemi specifici:

y - y₀ = m(x - x₀)

Dove m è un parametro che rappresenta la pendenza di una retta generica del fascio. Questa forma evidenzia immediatamente il centro del fascio (x₀, y₀) e rende più semplice lavorare con la pendenza delle rette.

Esempi Pratici

Vediamo alcuni esempi per chiarire come applicare la formula del centro del fascio:

Esempio 1: Trovare il centro del fascio di rette generato dalle rette r: x + y - 2 = 0 e s: 2x - y - 1 = 0.

Per trovare il centro, risolviamo il sistema:

{ x + y - 2 = 0 { 2x - y - 1 = 0

Sommando le due equazioni, otteniamo: 3x - 3 = 0, quindi x = 1. Sostituendo x = 1 nella prima equazione, otteniamo 1 + y - 2 = 0, quindi y = 1. Pertanto, il centro del fascio è il punto (1, 1).

Esempio 2: Trovare l'equazione della retta del fascio di rette di centro (2, -1) e passante per il punto (3, 1).

Sappiamo che l'equazione del fascio è della forma y - y₀ = m(x - x₀), dove (x₀, y₀) è il centro (2, -1). Quindi, l'equazione diventa y + 1 = m(x - 2). Per trovare il valore di m, sostituiamo le coordinate del punto (3, 1): 1 + 1 = m(3 - 2), quindi 2 = m. Pertanto, l'equazione della retta è y + 1 = 2(x - 2), che semplificata diventa y = 2x - 5.

Esempio 3 (Applicazione in Ingegneria Civile): Immagina di dover progettare un sistema di strade convergente verso un punto di controllo del traffico. Ogni strada può essere rappresentata come una retta. Il punto di controllo del traffico è il centro del fascio di rette. Conoscendo le equazioni di due strade esistenti, puoi determinare le coordinate del punto di controllo (il centro del fascio) e, quindi, pianificare l'orientamento delle nuove strade in modo che convergano in quel punto. Questo garantisce un flusso di traffico efficiente e sicuro.

Esempio 4 (Applicazione in Ottica): In ottica, i raggi luminosi possono essere modellati come rette. Un fascio di raggi luminosi che convergono verso un punto focale può essere rappresentato come un fascio di rette proprio. La posizione del punto focale è il centro del fascio. La comprensione di questo concetto è fondamentale nella progettazione di lenti e sistemi ottici.

Considerazioni Avanzate

L'uso del fascio di rette non si limita alla semplice individuazione del centro o alla determinazione di una retta specifica. Si può usare il fascio di rette per:

Conclusione

Il Centro del Fascio di Rette e la relativa formula sono concetti potenti e versatili nella geometria analitica. Comprendere a fondo questi concetti permette di risolvere una vasta gamma di problemi, dalle semplici intersezioni di rette a complesse applicazioni in ingegneria e fisica. Sperimenta con diversi esercizi e scenari per padroneggiare l'uso del fascio di rette e scoprire le sue potenzialità. Non sottovalutare la potenza di questo strumento! Esplora diverse risorse online e libri di testo per approfondire la tua conoscenza e affinare le tue capacità di risoluzione dei problemi.