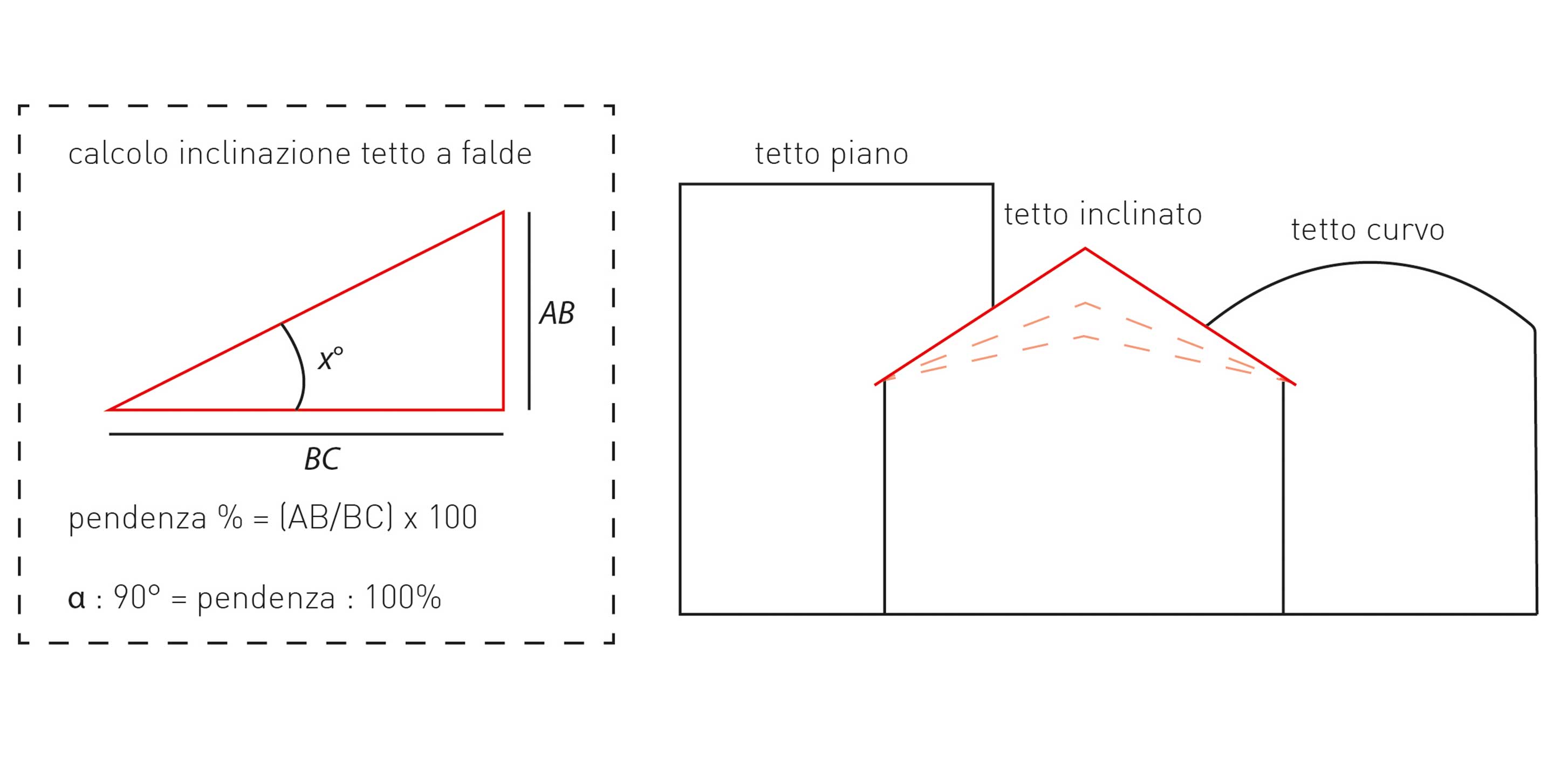
Calcolo Della Pendenza Di Una Rampa

Capita a tutti di bloccarsi di fronte a un concetto matematico. Magari sei lì, davanti a una rampa, e ti chiedi: "Come faccio a capire quanto è ripida? Come calcolo la pendenza?". Non preoccuparti, è una domanda comune e, con la giusta guida, la risposta diventa sorprendentemente chiara. Questa guida è pensata proprio per te, per rendere il calcolo della pendenza un'esperienza accessibile e, perché no, anche piacevole!

Cos'è la Pendenza? Una Definizione Intuitiva

La pendenza, in parole semplici, indica quanto una linea o una superficie è inclinata. Immagina una montagna: una montagna con una pendenza elevata è molto ripida, mentre una collina con una pendenza bassa è quasi pianeggiante. Matematicamente, la pendenza è un numero che esprime questo grado di inclinazione. Più grande è il numero, più ripida è la pendenza.

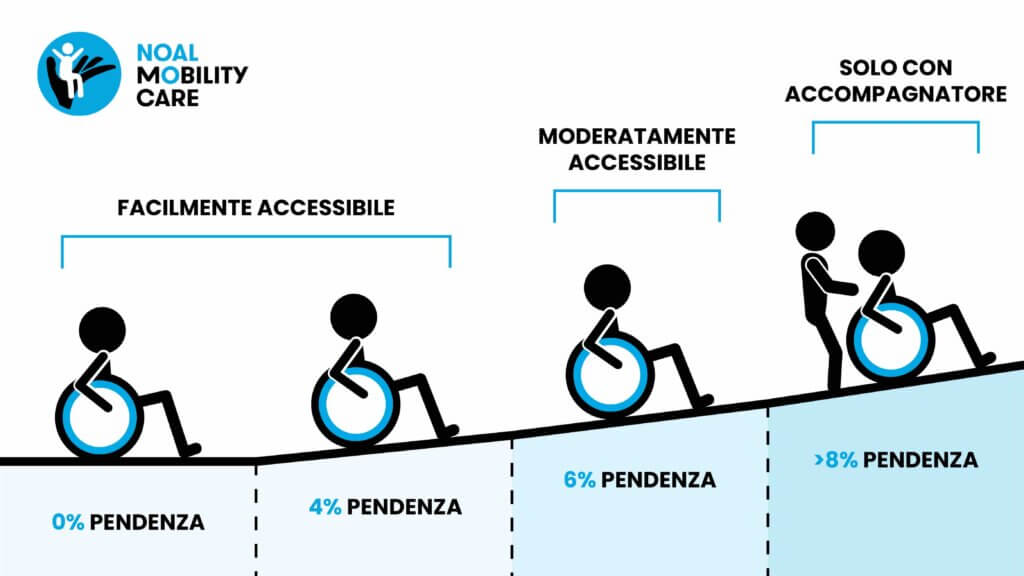
In ambito ingegneristico e architettonico, la pendenza è cruciale. Pensa alle rampe per disabili: la legge impone limiti precisi alla pendenza massima per garantire l'accessibilità e la sicurezza. Infatti, rampe troppo ripide possono essere pericolose e difficili da usare, soprattutto per persone con mobilità ridotta. Allo stesso modo, la pendenza delle strade influenza la sicurezza stradale e il consumo di carburante dei veicoli. Un articolo di ricerca pubblicato sulla rivista "Transportation Research Part D: Transport and Environment" (Bezić, H., & Petković, D. (2016). Impact of road gradient on vehicle fuel consumption and emissions: A review.) evidenzia proprio come la pendenza influenzi significativamente l'efficienza del trasporto.

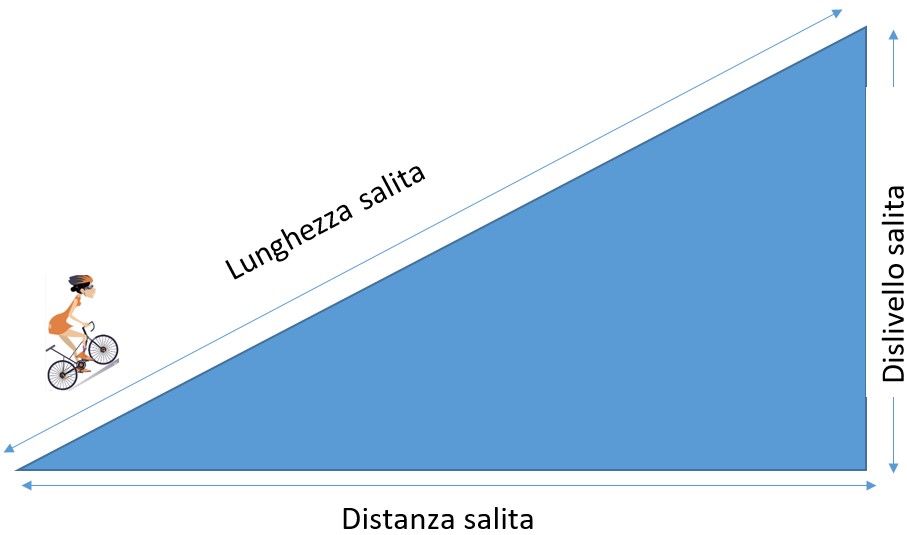
La Formula Magica: Il Rapporto Tra Variazione Verticale e Variazione Orizzontale

La formula per calcolare la pendenza è in realtà molto semplice: è il rapporto tra la variazione verticale (l'altezza) e la variazione orizzontale (la base). In termini matematici:

Pendenza (m) = Variazione Verticale / Variazione Orizzontale

Oppure, usando i termini più tecnici, ma altrettanto importanti:

m = Δy / Δx

Dove:

m rappresenta la pendenza.
Δy (delta y) rappresenta la variazione verticale, cioè la differenza di altezza tra due punti sulla rampa.
Δx (delta x) rappresenta la variazione orizzontale, cioè la distanza orizzontale tra gli stessi due punti.

Non farti spaventare dai simboli! Δy e Δx sono solo modi brevi per dire "differenza di altezza" e "differenza di distanza".

Come Calcolare la Pendenza di una Rampa: Passo Dopo Passo

Segui questi passaggi per calcolare la pendenza di una rampa in modo pratico:

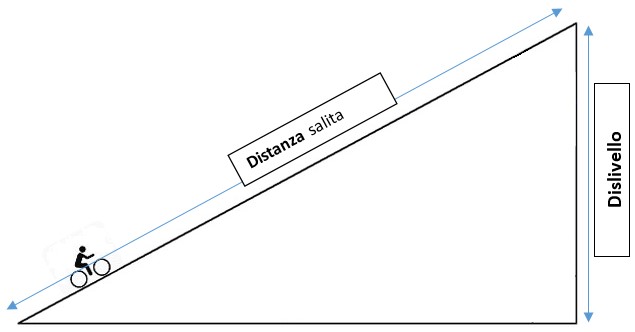
Misura l'altezza della rampa (Δy): Utilizza un metro o un misuratore laser per determinare la differenza di altezza tra il punto più basso e il punto più alto della rampa. Assicurati che l'unità di misura sia la stessa (es. metri o centimetri) per entrambe le misurazioni.
Misura la lunghezza orizzontale della rampa (Δx): Misura la distanza orizzontale tra il punto iniziale e il punto finale della rampa. Immagina di proiettare la rampa su un piano orizzontale: la lunghezza di questa proiezione è Δx.
Applica la formula: Dividi la variazione verticale (Δy) per la variazione orizzontale (Δx). Il risultato è la pendenza (m).
Esprimi la pendenza come percentuale (facoltativo): Moltiplica la pendenza (m) per 100. Questo ti darà la pendenza espressa come percentuale. Ad esempio, una pendenza di 0.15 corrisponde a una pendenza del 15%.

Esempio pratico:

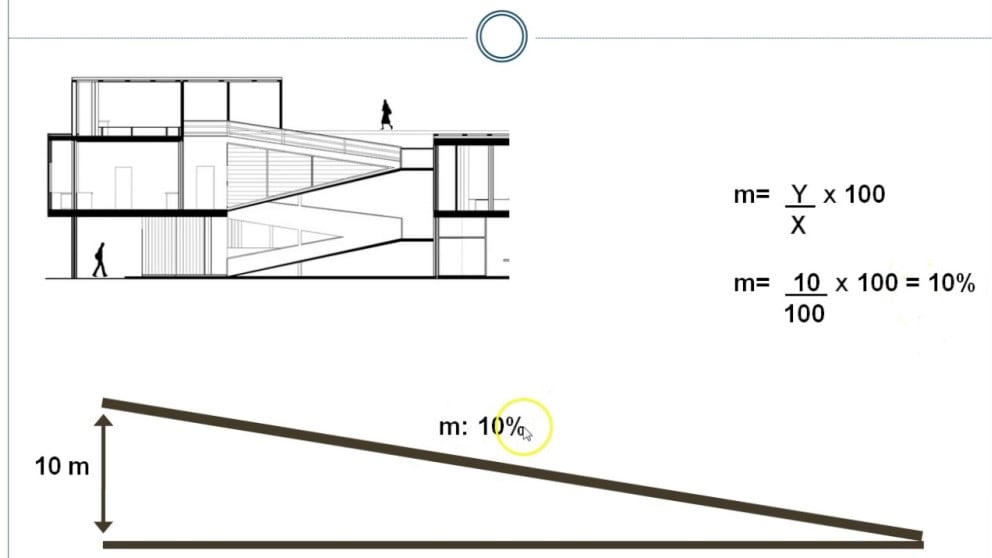
Supponiamo che una rampa abbia un'altezza di 0.5 metri (Δy = 0.5 m) e una lunghezza orizzontale di 5 metri (Δx = 5 m). La pendenza sarebbe:

m = 0.5 m / 5 m = 0.1

Per esprimere la pendenza come percentuale:

0.1 * 100 = 10%

Quindi, la pendenza della rampa è del 10%.

Pendenza Positiva, Pendenza Negativa e Pendenza Zero

La pendenza può essere positiva, negativa o zero. Cosa significano questi valori?

Pendenza positiva: La rampa sale da sinistra a destra. Questo significa che man mano che ti sposti in orizzontale, l'altezza aumenta.
Pendenza negativa: La rampa scende da sinistra a destra. Questo significa che man mano che ti sposti in orizzontale, l'altezza diminuisce.
Pendenza zero: La rampa è orizzontale. Non c'è variazione di altezza.

Una linea verticale ha una pendenza indefinita, perché la variazione orizzontale (Δx) è zero, e la divisione per zero non è definita in matematica.

Errori Comuni da Evitare

Ecco alcuni errori comuni che è bene evitare quando si calcola la pendenza:

Utilizzare unità di misura diverse: Assicurati che sia l'altezza che la lunghezza orizzontale siano misurate nella stessa unità (es. metri o centimetri).
Confondere l'altezza con la lunghezza della rampa: L'altezza è la variazione verticale, mentre la lunghezza della rampa è la distanza effettiva lungo la superficie inclinata. Per il calcolo della pendenza, è necessaria la lunghezza orizzontale.
Invertire la formula: Ricorda, la pendenza è sempre la variazione verticale divisa per la variazione orizzontale (Δy / Δx), non il contrario.

Consigli Pratici per l'Insegnamento e l'Apprendimento

Se sei un insegnante, un genitore o uno studente, ecco alcuni consigli utili per rendere l'apprendimento del concetto di pendenza più efficace:

Usa esempi concreti: Invece di concentrarti solo sulla teoria, mostra agli studenti esempi reali di rampe, strade, tetti e altre superfici inclinate.
Utilizza strumenti di misurazione: Coinvolgi gli studenti nella misurazione pratica dell'altezza e della lunghezza orizzontale di diverse rampe.
Crea attività interattive: Utilizza software o app online per creare simulazioni di rampe con diverse pendenze e permetti agli studenti di sperimentare con i parametri.
Collega la pendenza ad altri concetti matematici: Mostra come la pendenza è correlata ad altri concetti come l'angolo di inclinazione, la trigonometria e le funzioni lineari.
Rendi l'apprendimento divertente: Organizza giochi o sfide in cui gli studenti devono calcolare la pendenza di diverse rampe o superfici.

Ad esempio, potresti organizzare una caccia al tesoro in cui gli indizi sono nascosti su oggetti con diverse pendenze. Gli studenti devono calcolare la pendenza per trovare l'indizio successivo. Questo rende l'apprendimento più coinvolgente e memorabile.

Incoraggia l'esplorazione: Permetti agli studenti di esplorare il concetto di pendenza in modo autonomo. Incoraggiali a fare domande, a sperimentare e a commettere errori. L'errore è una parte importante del processo di apprendimento.

Conclusione: La Pendenza, un Concetto alla Portata di Tutti

Il calcolo della pendenza di una rampa può sembrare complicato all'inizio, ma con la giusta comprensione dei concetti di base e un po' di pratica, diventa un'operazione semplice e accessibile a tutti. Ricorda: non aver paura di fare domande e di sperimentare! La matematica è un linguaggio che si impara con la pratica e la curiosità. Con questa guida, hai tutti gli strumenti necessari per affrontare con sicurezza il calcolo della pendenza e applicarlo a situazioni reali.

Ricorda che la comprensione della pendenza non è solo un esercizio matematico, ma una competenza utile nella vita di tutti i giorni. Che tu stia progettando una rampa, costruendo un modello, o semplicemente cercando di capire quanto è ripida una collina, la capacità di calcolare la pendenza ti darà una nuova prospettiva sul mondo che ti circonda. Quindi, continua a esplorare, a imparare e a mettere in pratica le tue conoscenze!