Bisettrice Primo E Terzo Quadrante Equazione

Ciao! So che molti studenti trovano un po' ostica la bisettrice del primo e terzo quadrante. Niente panico! È un concetto più semplice di quanto sembri. Cerchiamo di capirlo insieme, passo dopo passo. L'obiettivo è rendere tutto chiaro e memorizzabile, senza inutili complicazioni.

Cos'è la Bisettrice del Primo e Terzo Quadrante?

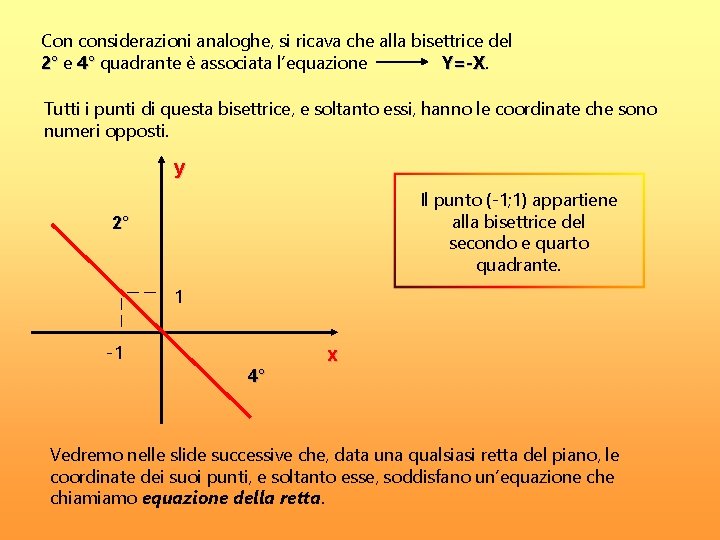
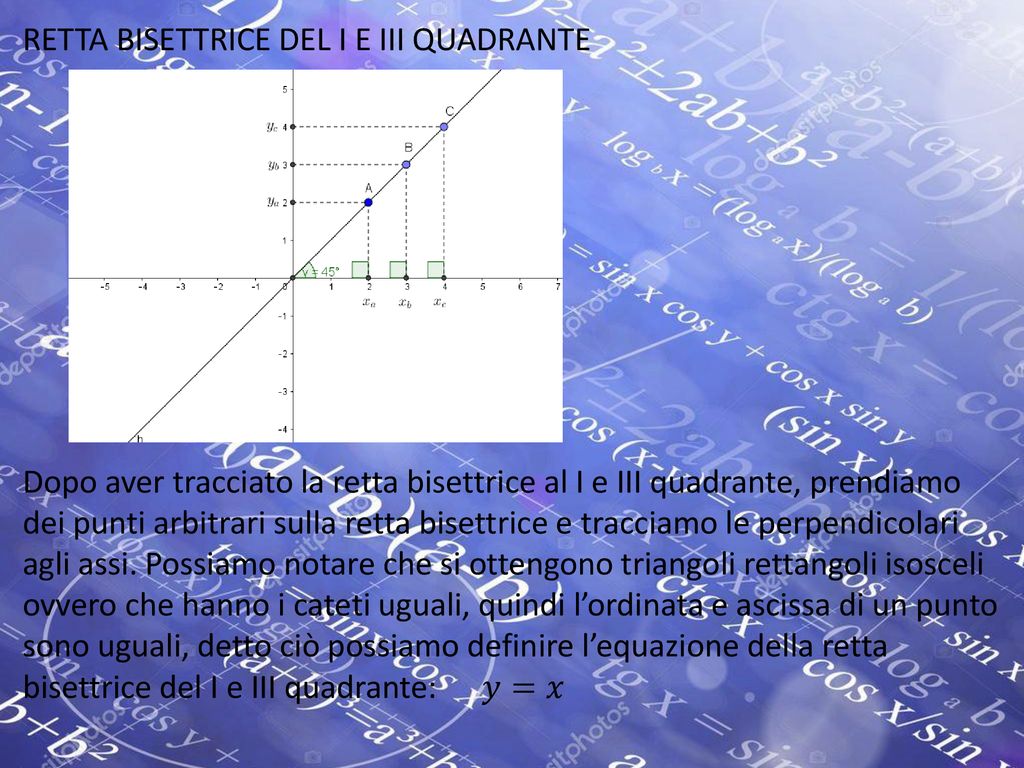
Immagina un piano cartesiano, quello con l'asse delle x (orizzontale) e l'asse delle y (verticale). Questo piano è diviso in quattro quadranti. La bisettrice del primo e terzo quadrante è semplicemente una retta che taglia a metà l'angolo formato dagli assi nei quadranti 1 e 3. In altre parole, divide l'angolo di 90 gradi in due angoli di 45 gradi.

Perché è importante?

Ti starai chiedendo: "Ok, ma a cosa serve?". Beh, questa bisettrice è un riferimento fondamentale in geometria analitica. La sua equazione è incredibilmente semplice e ci aiuta a capire le relazioni tra le coordinate dei punti nel piano. Conoscere la sua equazione permette di risolvere più velocemente alcuni esercizi.

L'Equazione Fondamentale: y = x

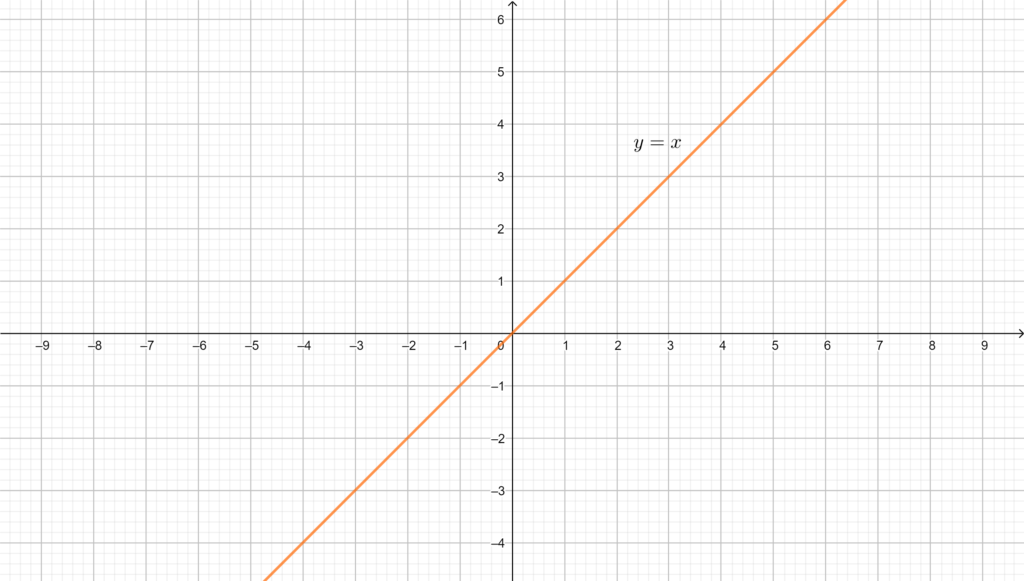
Ecco la magia: l'equazione della bisettrice del primo e terzo quadrante è:

y = x

Semplicissimo, vero? Cosa significa? Vuol dire che ogni punto che si trova su questa retta ha la coordinata x uguale alla coordinata y. Ad esempio, il punto (2, 2) si trova sulla bisettrice, così come il punto (-3, -3). In sostanza, se disegnassi tutti i punti dove l'ascissa è uguale all'ordinata, otterresti proprio la nostra bisettrice.

Verifica Pratica

Prendiamo un punto a caso, ad esempio (5, 5). Se sostituiamo questi valori nell'equazione y = x, otteniamo 5 = 5. L'uguaglianza è verificata, quindi il punto appartiene alla bisettrice. Proviamo ora con un punto che non appartiene alla bisettrice, ad esempio (1, 4). Sostituendo otteniamo 4 = 1, che è ovviamente falso. Questo conferma che il punto (1, 4) non si trova sulla bisettrice.

Come Usare questa Informazione nei Problemi

Capire l'equazione y = x può semplificarti la vita in molti esercizi di geometria analitica. Ad esempio, se un problema ti dice che un punto si trova sulla bisettrice del primo e terzo quadrante, sai immediatamente che la sua ascissa e la sua ordinata sono uguali. Questo ti permette di ridurre le incognite e risolvere il problema più facilmente.

Supponiamo di dover trovare l'intersezione tra una retta e la bisettrice del primo e terzo quadrante. Invece di avere due incognite (x e y), ne hai solo una, perché sai che y = x. Puoi quindi sostituire x al posto di y (o viceversa) nell'equazione della retta e risolvere l'equazione risultante.

Esercizio Guidato

Trova l'intersezione tra la retta di equazione y = 2x - 1 e la bisettrice del primo e terzo quadrante.

Sappiamo che sulla bisettrice y = x. Quindi, possiamo sostituire x al posto di y nell'equazione della retta: x = 2x - 1.

Risolvendo per x, otteniamo: x = 1.

Dato che y = x, anche y = 1.

Quindi, il punto di intersezione è (1, 1).

Un Ultimo Consiglio

Ricorda, la matematica è come un linguaggio: più la pratichi, più diventa fluente. Non aver paura di fare errori, sono parte del processo di apprendimento. E non dimenticare: y = x. Ripetilo a te stesso finché non ti entra in testa!

Spero che questa spiegazione ti sia stata utile. In bocca al lupo con i tuoi studi!